题目大意:皇宫有n个宫殿,呈一棵树的形状,在一个宫殿布置侍卫,可以看守到道路对面的宫殿,不同宫殿布置侍卫经费有所不同,所有宫殿都被看守,最少经费是多少?
描述
huyichen世子事件后,xuzhenyi成了皇上特聘的御前一品侍卫。
皇宫以午门为起点,直到后宫嫔妃们的寝宫,呈一棵树的形状;某些宫殿间可以互相望见。大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是xuzhenyi手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助xuzhenyi布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
格式
输入格式
输入文件中数据表示一棵树,描述如下:
第1行 n,表示树中结点的数目。
第2行至第行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号i(),在该宫殿安置侍卫所需的经费k,该点的儿子数m,接下来m个数,分别是这个节点的m个儿子的标号。
对于一个n()个结点的树,结点标号在1到n之间,且标号不重复。保证经费总和不超过。
输出格式
输出文件仅包含一个数,为所求的最少的经费。
样例1
样例输入1
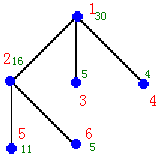
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
样例输出1
25
限制
提示
解题思路
树形DP,每一个结点,有3中状态,1是布置侍卫,整棵子树都被看守了;0是不布置侍卫,但整个子树还是都被看守了(至少一个儿子结点布置了侍卫);2是不布置侍卫,但所有儿子子树都被看守了。
搜索过程赋初值:f[i][0]不布置侍卫,初始为0,但如果是叶子结点,则为无穷大,因为叶子结点必须布置侍卫该子树才能被看守;f[i][1]布置侍卫的经费v[i],然后累加儿子子树经费;f[i][2]不布置侍卫经费为0,然后累加儿子子树经费。
状态转移:父亲结点是a,儿子结点是b,那么f[a][1] += min(f[b][0], f[b][1], f[b][2]),因为布置了侍卫,只要满足孙子子树已经被看守就行了;f[a][0] += min(f[b][0], f[b][1]),需要注意的是,如果儿子中f[b][0]全是小的,那么要选一个来布置侍卫,这样父亲结点a才能被看守,如果要选,就算经费差(f[b][1]-f[b][0])最小的儿子结点,代码中z记录最小经费差,如果出现f[b][1]小的情况,z=0(代码19行);f[a][2] += min(f[b][0], f[b][1]),因为f[a][2]只需要满足孙子子树被看守,因此,儿子既可以布置侍卫,也可以不布置侍卫,如果写成f[a][2] += f[a][0]就会出错,暂时没想反例,可能是初值设定、累加超过变量范围等原因造成的吧。
程序实现

无穷大的设定,到达该多大?太大加一点点容易爆int,太小有可能小于结点经费值,那就设定为节点经费值吧!因为如果再大,也不应该超过结点经费,只要在结点布置了侍卫,其儿子都能够被看守,也相当于选了一个儿子布置了侍卫。
