题目大意:n个有长度的物品,选出两堆,使得他们总长度相等,输出最长的长度。
描述
2001年9月11日,一场突发的灾难将纽约世界贸易中心大厦夷为平地,Mr. F曾亲眼目睹了这次灾难。为了纪念“9?11”事件,Mr. F决定自己用水晶来搭建一座双塔。
Mr. F有N块水晶,每块水晶有一个高度,他想用这N块水晶搭建两座有同样高度的塔,使他们成为一座双塔,Mr. F可以从这N块水晶中任取M(1≤M≤N)块来搭建。但是他不知道能否使两座塔有同样的高度,也不知道如果能搭建成一座双塔,这座双塔的最大高度是多少。所以他来请你帮忙。
给定水晶的数量N(1≤N≤100)和每块水晶的高度Hi(N块水晶高度的总和不超过2000),你的任务是判断Mr. F能否用这些水晶搭建成一座双塔(两座塔有同样的高度),如果能,则输出所能搭建的双塔的最大高度,否则输出“Impossible”。
格式
输入格式
输入的第一行为一个数N,表示水晶的数量。第二行为N个数,第i个数表示第i个水晶的高度。
输出格式
输出仅包含一行,如果能搭成一座双塔,则输出双塔的最大高度,否则输出一个字符串“Impossible”。
样例1
样例输入1
样例输出1
来源
某校NOIP模拟题
解题思路
本题是动态规划经典题目,既可以用搜索解决,也可以用动态规划解决。
对于动态规划,需要定义状态f[i][j]表示前i个物品组成两条“龙”,长度之差为j时的最长长度,长度越长越好,在同等情况下可以选择最优值。
程序实现
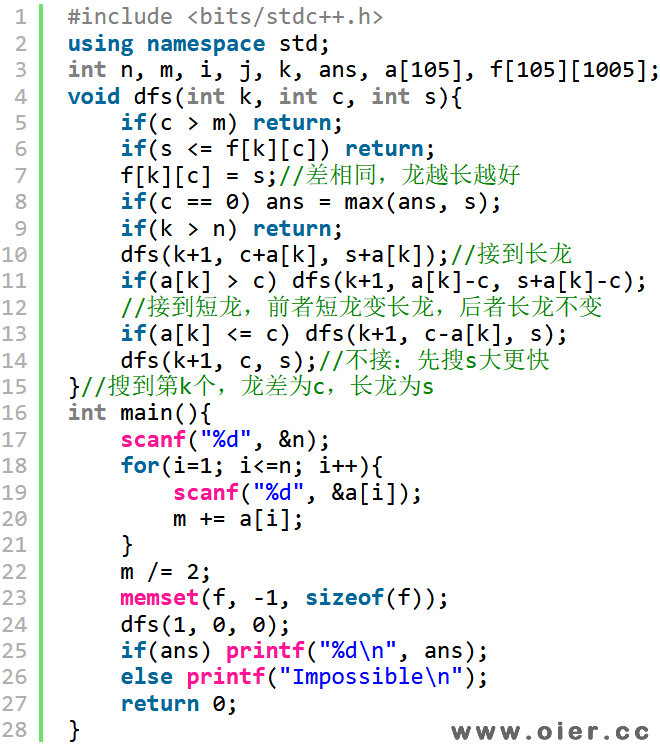
爆搜加记忆化:对于每个物品,要么不要(不接龙),要么接在某条龙上(龙1或者龙2)。不加记忆化,时间复杂度是O(3^n)。不难发现,对于前k个物品,如果得到的两条龙的长度跟之前重复,就不需要搜索下去,故我们可以加个记忆化,类似Flood Fill,在搜索过程中,同一种状态搜过不需要再搜。题目说总长度不超过2000,故龙的长度不能超过1000,开数组f[i][j][k]记录前i个物品,龙1长x,龙2长y的搜索状态,搜过不再搜,时间复杂度降为O(n*1000*1000),数组开char不会超空间。

如果总长度再大一些,或者n再大一点,必会超内存,而且很容易超时,我们可以采用记忆化剪枝,如何将3维数组降成2维?将某一维度放到值里面?
f[数量][龙1] = 龙2?f[龙1][龙2] = 数量?都不好,无法比较好坏。对于两条龙,只需要知道一条龙的长度和差,就可以求出另外一条龙。对于查相同的时候,龙越长越好。
我们可以用f[数量][龙差] = 长龙长度来进行记忆化剪枝。随着函数参数的变化,稍微改动一下搜索的程序即可。这样程序比之前快至少10倍!
再加入启发式搜索,速度可以再快100倍!对于第10-14行,搜索的顺序并不是随意的,先搜索长龙长度大的,这样后面搜索的长龙长度小的可能性更多,剪枝剪得更多。
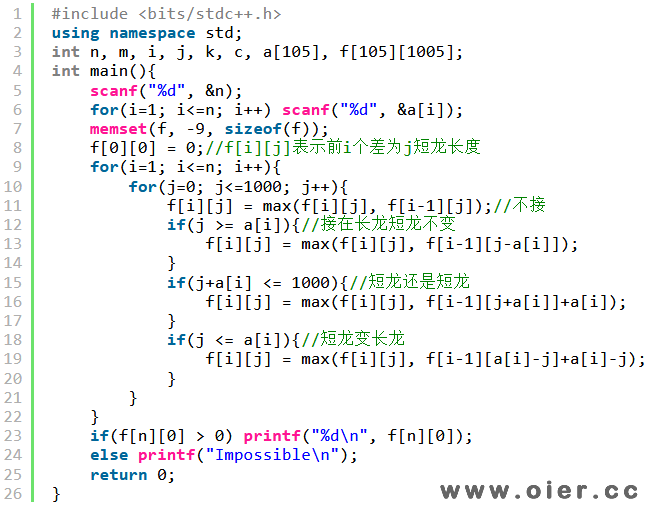
既然定义出状态了,不妨试试动态规划,下面代码是从前往后推:

以下代码是为求出f[i][j],同上一步f[i][k]转移过来:

定义f[i][j]表示前i个差为j的短龙最长长度也可以做: