题目大意:已知n个点的位置,请在X轴选择一个最小的长度,让这个范围内点的Y坐标之差达到m。
【问题描述】
FJ一直苦于无法让他的植物生长,需要你的帮助给植物适当地浇水。现在给你2D平面上N个雨水落下的位置 (1 <= N <= 100,000),y代表雨水落下的垂直高度,x代表横向坐标:
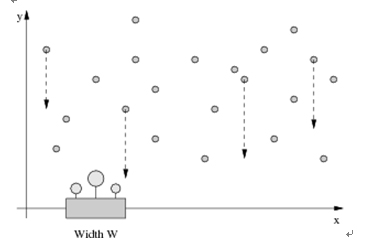
每一滴雨水朝着X轴方向以每秒1个单位的速度下落。FJ想要把宽度为W的花盆沿着X轴移动到某个位置,以保证第一滴雨水落入花盆的时间和最后一滴雨水落入花盆的时间的差至少是D,(这样就能让花盆里的花获得大量的雨水)砸到花盆边缘的雨水也视为落入了花盆。
给出D的值以及N滴雨水的位置,请计算出W的最小值。
【输入格式】
第1行:两个用空格隔开的整数N 和D. (1 <= D <= 1,000,000)
第2..N+1行: 第 i+1 行(xi,yi)表示雨点i的初始位置 (0<=xi, yi<=1,000,000)
【输出格式】
一个整数,表示最小的花盆宽度。如果找不到这个方案,输出“-1”。
【输入样例】
4 5
6 3
2 4
4 10
12 15
【输出样例】
2
样例解释:一个宽度w为2的花盆,如果放在x=4..6,那么它可以接到第1,第3滴雨水,总共间隔为10-3=7,满足>=5。
解题思路
长度t满足要求,那么长度t+1更加满足要求;长度t不满足要求,那么长度小了更加不满足要求,具备二分查找的性质,可以稍微减轻思考难度。
程序实现
对于选择的长度区间[l, r],l和r,必定一个是最大值,一个是最小值,如果是中间值,那么这个位置可以不要,长度更小。
也就是说,最小值要么在左边,要么在右边。我们可以分开两种情况处理。
如果最小值在左边,那么下一个点更大就入队,队头和队尾的差值满足要求就行。如果下一个点更小,那么之前大的点从队尾出队,因为他不可能作为开头了。队列中只存储可能的区间左端点,维护单调递增的性质即可。
最小值在右边,同理可以解决。
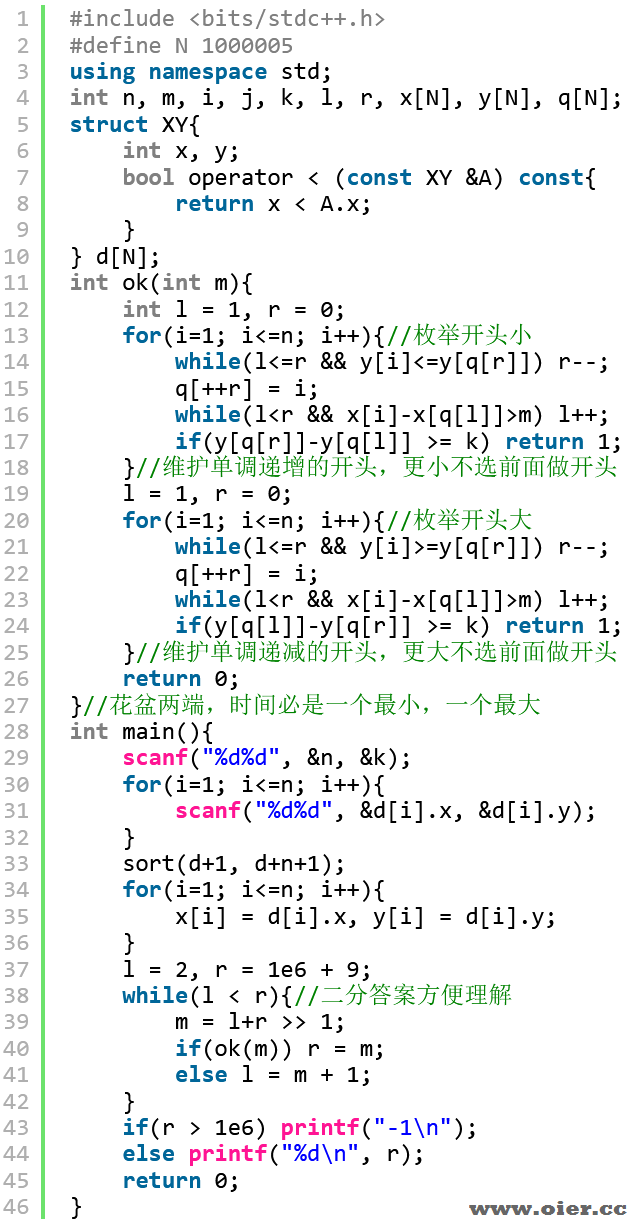
每次验证,都做了很多重复的内容,其实可以直接双指针尺取法解决。
枚举开头小,同样维护单调递增的队列,每次入队,只要发现满足要求,就记录最小长度,并把队头出队,因为他已经找到最合适的右端点了。这样,一遍扫过去,每个左端点都找到了自己最近的符合要求的右端点。
