SSOJ3014B森近霖之助
3681+
作者：crxis 发布：2019-04-28 分类：位运算
题目大意：一个机器打印纸条，根据纸条上的0和1打印出对应的或、与、抑或值，至少需要多少条纸条才能确定机器每一位到底是或、与还是抑或呢？
题目描述
森近霖之助捡到了一台奇怪的机器。往里面塞进去两条固定长度的打孔纸带，就会吐出一条同样长度的打孔纸带。打印出来的纸带是没法放进机器里的。
在经过一段时间的思索之后，霖之助发现了这台机器的输出具有一定的规律。具体而言，输出的每一位都是输入两个打孔纸带上同样位置值的“与”，“或”或者“异或”。
拿着手中的纸带，若有所思的霖之助想要知道，他最少要自己制作多少条新的打孔纸带，才能知道这台机器的确切工作方式？
输入
第一行，包含一个整数 N ，表示已有纸带的数目。
接下来 N 行，每行包含一个字符串，表示已有的纸带的情况。
输出
一行，包含一个数，需要自己制作的纸带数。
样例输入
2
01010101
10101010
样例输出
1
提示
•对于分值为 40 的子任务 1，保证 N ≤ 50，纸带长度 ≤ 10
•对于分值为 60 的子任务 2，保证 N ≤ 50，纸带长度 ≤ 100。
解题思路
把与、或、异或的真值表写出来就很容易找到规律：
如果两个都是1，打印出0可以判断是异或；
如果两个都是0，打印处理都是0，无法判断任何信息；
如果有0和1，打印出0可以判断是与。
也就是说，只要有11和01，就可以判断出是异或和与，都不是就是或。
至少需要3条纸条，就可以保证每一列都有1个0和2个1。
还需要多少纸条，就看每一列到底差什么：没有0加1条，没有1加2条，1个1加1条。
因为每一列都需要确定，所以去最大值。
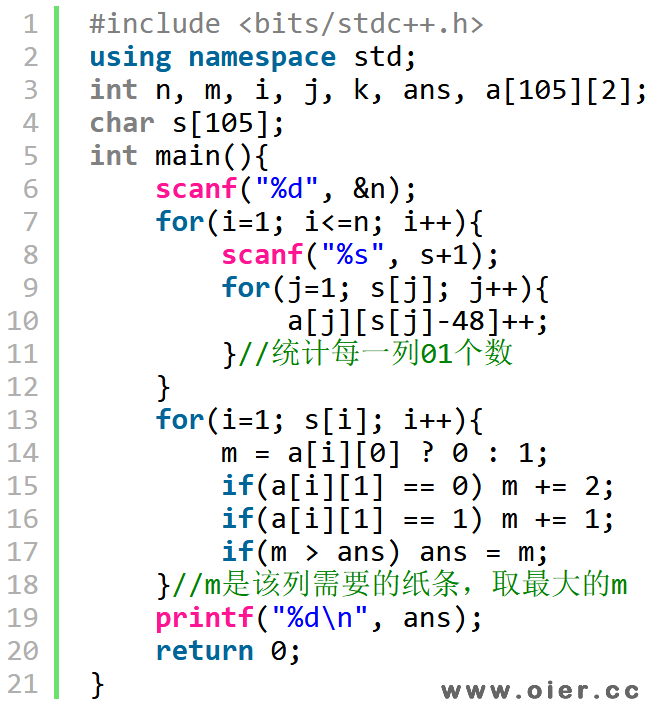
程序实现
