题目大意:给定一棵二叉树,输出它最大的对称子树的结点个数;所谓对称,就是将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
题目描述
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
1. 二叉树;
2. 将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
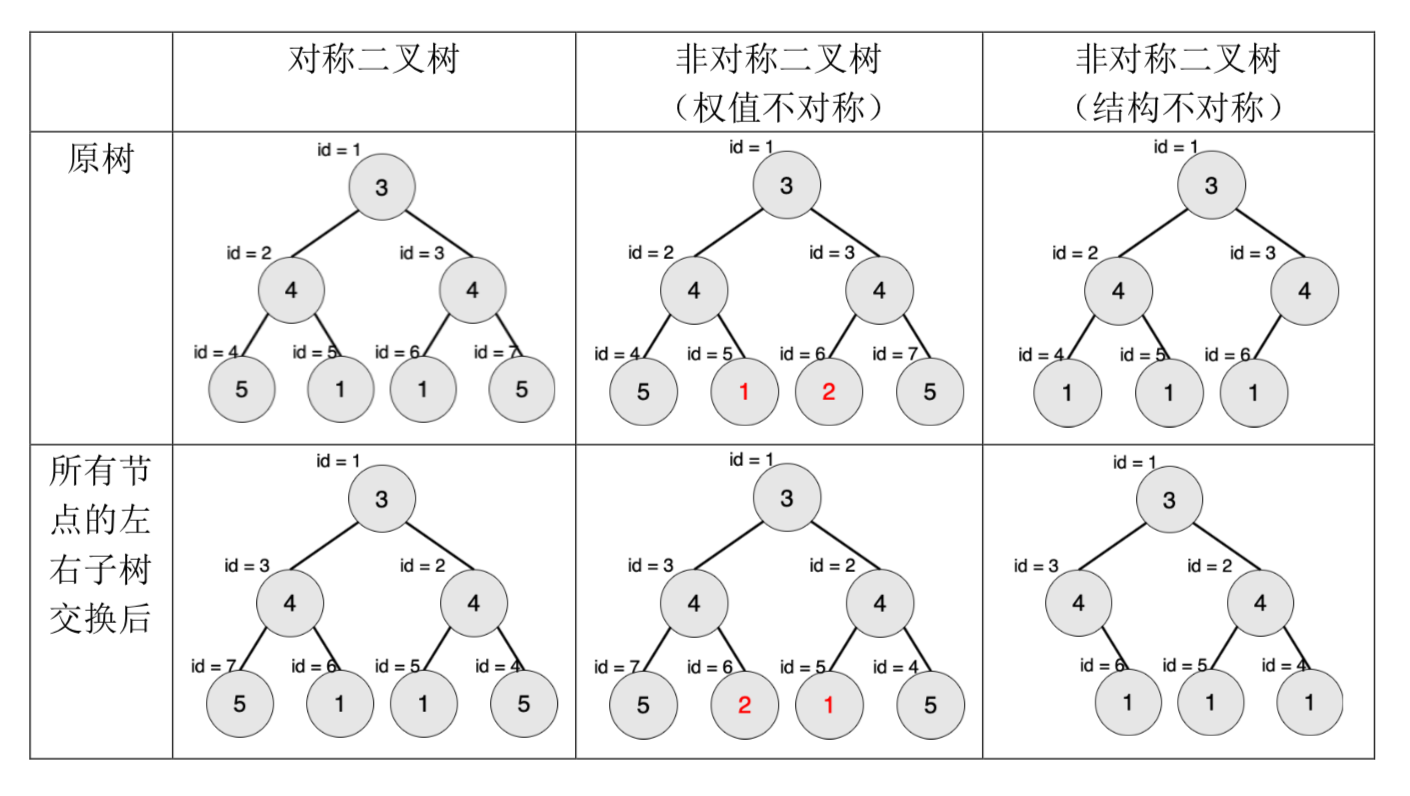
现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数 最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。本题中约定,以节点 T为子树根的一棵“子树”指的是:节点T和它的全部后代节点构成的二叉树。
本题约定: 层次:节点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一节
点的层次等于其父亲节点的层次加 1。 树的深度:树中节点的最大层次称为树的深度。
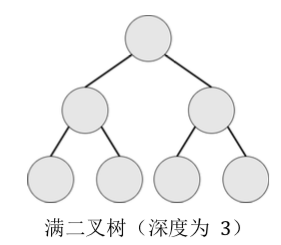
满二叉树:设二叉树的深度为 h,且二叉树有 2h − 1 个节点,这就是满二叉树。
个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
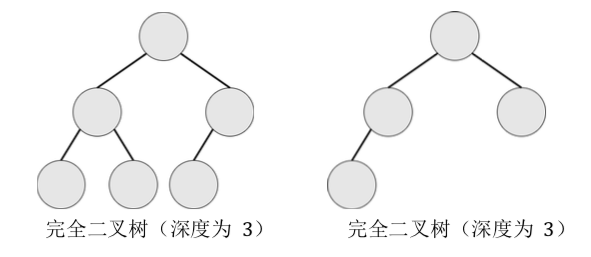
输入
第一行一个正整数
输出
输出文件共一行,包含一个整数,表示给定的树的最大对称二叉子树的节点数。
样例输入
样例1:
2
1 3
2 -1
-1 -1
样例2:
10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8
样例输出
样例1:1
样例2:3
提示
样例1说明:
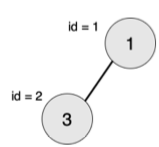
最大的对称二叉子树为以节点 2 为树根的子树,节点数为 1。
样例2说明:
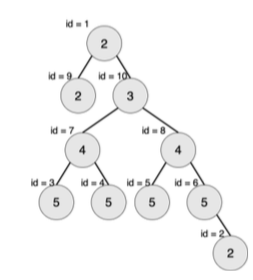
最大的对称二叉子树为以节点 7 为树根的子树,节点数为 3。
共 25 个测试点。
解题思路
如果一棵子树是对称的,那么他的中序变量和逆中序遍历是相同的,也就是子树的DFS序是回文串。
需要注意的是,不同层次结点是值有可能相同,这样儿子在左边或者右边就判断不出来(父亲结点的值跟儿子一样),因此,我们可以给结点的值加入层次,如加上层次*1003(超过权值的范围)。
处理好DFS序和子树结点数量后,跑一遍Manacher匹配最大回文串,如果回文长度跟子树结点数量相等,那么就是对称子树,记录最大值。
其他方法:哈希(有冲突怎么办?)、爆搜(怎么剪枝?)等也可以尝试。
程序实现
