题目大意: $N$ 个节点的有向无环图,图中某些节点上有棋子,两名玩家交替沿有向边移动棋子,不能移动算输,请问先手是否有必胜策略?
给定一个有 $N$ 个节点的有向无环图,图中某些节点上有棋子,两名玩家交替移动棋子。
玩家每一步可将任意一颗棋子沿一条有向边移动到另一个点,无法移动者输掉游戏。
对于给定的图和棋子初始位置,双方都会采取最优的行动,询问先手必胜还是先手必败。
【输入】
第一行,三个整数 $N , M, K$, $N$ 表示图中节点总数, $M$ 表示图中边的条数, $K$ 表示棋子的个数。
接下来 $M$ 行,每行两个整数 $X, Y$ 表示有一条边从 $X$ 出发指向 $Y$。
接下来一行, $K$ 个空格间隔的整数,表示初始时,棋子所在的节点编号。
【输出】
若先手胜,输出 $win$,否则输出 $lose$。
【输入样例】
6 8 4 2 1 2 4 1 4 1 5 4 5 1 3 3 5 3 6 1 2 4 6
【输出样例】
win
【提示】
数据范围与提示:
对于全部数据, $N≤2000,M≤6000,1≤K≤N$。
解题思路
注意:棋子好像可以移动到同一个位置?
将棋子结点转换成一堆石子,石子数量即mex值。
对于没有出边的结点,mex值为0,相当于一堆数量为0的石子,无法操作。
对于有出边的节点,mex值为他能到的所有结点的mex值中,最小未出现过的值,因为这是“最优”的。
不妨设结点能到达mex值为0、1、2、3、5、6、8、9的结点,那么该结点mex值取4。首先,取4比取小于4的优,因为选择更多,且4是合法的,因为他可以“取任意多个石子”,到达状态0、1、2、3;其次,取更大的也没必要,如果取更大的,要么下一步取到比4小(4也可以实现),要么取到比4大(对手可以让我变为4),都不比4好。
注意,第一次取石子,只能到达后继状态,即使看成是一堆石子有7个,也只能走到0、1、2、3、5、6等状态,之后才可以任意走。
这样,算出每个结点的mex值后,就可以转换为异或和非零必胜了,因为他就跟取石子一样了。
程序实现
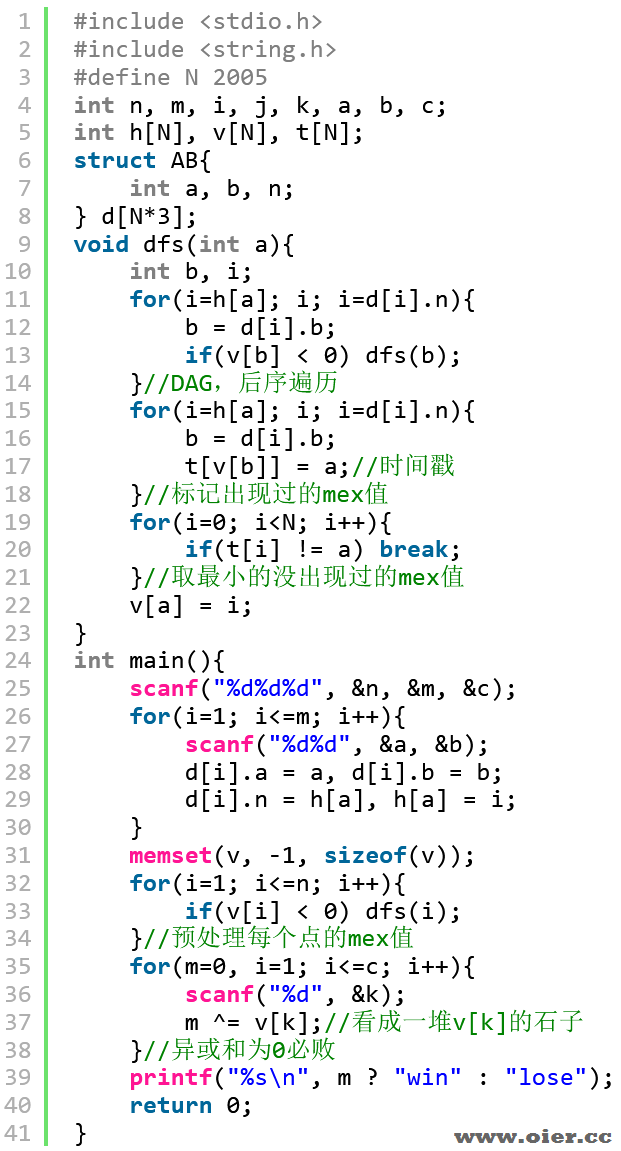
原来是这样用的 😉