SSOJ2923Fibonacci前n项和
1833+
作者：crxis 发布：2020-12-30 分类：矩阵
题目大意：求Fibonacci前n项和，n很大，怎么快速求解？
题目描述
大家都知道 Fibonacci 数列吧，f1=1,f2=1,f3=2,f4=3,…,fn=fn−1+fn−2。
现在问题很简单，输入 n 和 m，求 {fn} 的前 n 项和 Snmodm。
输入
输入 n,m。
输出
输出前 n 项和 Snmodm。
提示
样例输入
5 1000样例输出
12对于 100% 的数据， 1≤n≤2×109,1≤m≤109+10。
解题思路
前n项：1 1 2 3 5 8 13 21 34 …
前n项和：1 2 4 7 12 20 33 …
上下一看，发现$s_n = f_{n+2} – 1$，套用上一题的矩阵快速幂即可。
程序实现
当然，不是所有题目都有这么明显的规律，我们也可以尝试推一下，退出多种矩阵乘法！
他们中有fn、sn，那么他们与前一项有什么关系呢？
$s_n = s_{n-1} + f_n$，$f_n = f_{n-1} + f_{n-2}$
可以得到：$s_n = s_{n-1} + f_{n-1} + f_{n-2}$。
设一个三行一列的矩阵：
$s_n$
$f_{n}$
$f_{n-1}$
希望下一次能够推出：
$s_{n+1}$
$f_{n+1}$
$f_{n}$
那么需要左边乘上一个矩阵T：
1 1 1
0 1 1
0 1 0
乘n-1次，即可得到sn。如何求矩阵T的n-1次方？需要用到单位矩阵：
1 0 0
0 1 0
0 0 1
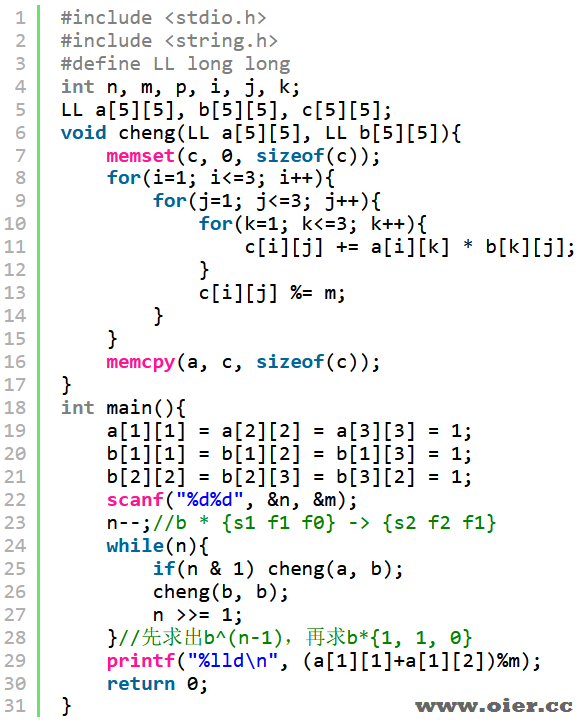
当然，还有其他各种矩阵可以解决这个问题。我们需要做的，就是自己思考出来，无论题目怎么变都能想出方法解决。