题目大意:一个整数n,模$a_1$余数是$b_1$,模$a_2$余数是$b_2$,模$a_3$余数是$b_3$,请问n是多少?
题目描述
自从曹冲搞定了大象以后,曹操就开始琢磨让儿子干些事业,于是派他到中原养猪场养猪,可是曹冲很不高兴,于是在工作中马马虎虎,有一次曹操想知道母猪的数量,于是曹冲想狠狠耍曹操一把。
举个例子,假如有 16 头母猪,如果建了 3 个猪圈,剩下 1 头猪就没有地方安家了;如果建造了 5 个猪圈,但是仍然有 1 头猪没有地方去;如果建造了 7 个猪圈,还有 2 头没有地方去。你作为曹总的私人秘书理所当然要将准确的猪数报给曹总,你该怎么办?
输入
第一行包含一个整数 n,表示建立猪圈的次数;
接下来 n 行,每行两个整数 $a_i, b_i$,表示建立了 $a_i$ 个猪圈,有 $b_i$ 头猪没有去处。你可以假定 $a_i,a_j$ 互质。
输出
输出仅包含一个正整数,即为曹冲至少养猪的数目。
提示
样例输入
3
3 1
5 1
7 2样例输出
16解题思路
暴力翻倍:因为模数不超过1000,所以翻倍次数不多,时间复杂度是$O(\sum{a_i})$。
中国剩余定理:因为模数互质,逆元存在,所以可以使用中国剩余定理。翻多少倍?其余方程的模数之积的倍数,不会影响其他方程的解;再乘以这个倍数的逆元,不影响自己方程的解。
扩展欧几里得:合并同余方程。X%a=r,X%b=t,令X = ax+r = -by+t,那么ax+by = t-r,解这个方程即可得到X=ax+r,下次翻倍为lcm(a, b),即转换成模lcm(a, b)余X。
程序实现
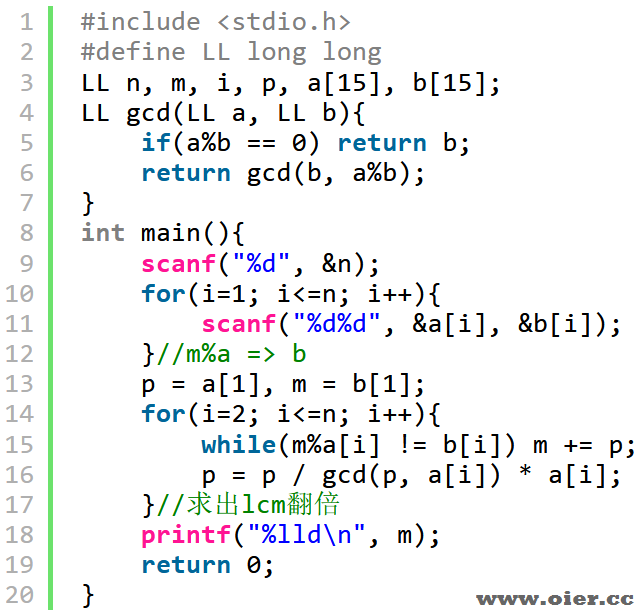
暴力翻倍:首先b[1]满足方程1,不断地加a[1]也满足方程1,加到满足方程2的时候,下次累计lcm(a[1], a[2])即可。这样做n次,就可以满足n个方程了。
中国剩余定理:t=M/a[i]是其他方程的模数之积,加上这个数不影响其他方程的余数;x是t的逆元,x*t*b%a还是b。这样每个方程都是余b了。
注意:t和x都很大,可以先模a[i],避免相乘溢出。

扩展欧几里得:代入方程求解即可。题目保证有解,直接求ax+by=t-r,最终令x=t-r即可。若非互质,令x=(t-r)/a,y=0,最终代入判断即可确定是否有解。
