SSOJ2905反素数Antiprime[一本通][POI2001]
1834+
作者：crxis 发布：2021-01-13 分类：数学
题目大意：不超过n的最大反素数是多少？所谓反素数，就是（自己以内）约数个数最多的数字。
题目描述
原题来自：POI 2001
如果一个大于等于 1 的正整数 n，满足所有小于 n 且大于等于 1 的所有正整数的约数个数都小于 n 的约数个数，则 n 是一个反素数。譬如：1,2,4,6,12,24，它们都是反素数。
请你计算不大于 n 的最大反素数。
输入
一行一个正整数 n。
输出
只包含一个整数，即不大于 n 的最大反素数。
提示
样例输入
1000样例输出
840对于 10% 的数据，1≤n≤103；
对于 40% 的数据，1≤n≤106；
对于 100% 的数据，1≤n≤2×109。
解题思路
暴力枚举每个质因子的次幂，这个数不能超过n，而且是反素数。
显然，我们会尽量选择小的质因子，因为如果质因子小，可以多乘几个，约数更多；另外，我们也希望质因子种类多一点，因为约数个数等于各个质因子次幂加1相乘。
基于这个原则，我们会发现，这个数的质因子肯定都是从小打到开始选择的，当第一个质因子次幂比较高的时候，就可以选下一个质因子，而且不会跳着选，因为如果选择一个更大的质因子，总可以将这个质因子换成小的，从而实现约数个数一样但数字更小。
结论：质因子从小到大连续，且后面的质因子次幂不超过前面的！因为超过的话，可以交换一下，约数个数一样且更小。
最后爆搜的时候，确定每个质因子的范围即可，如果乘积超过n结束递归。
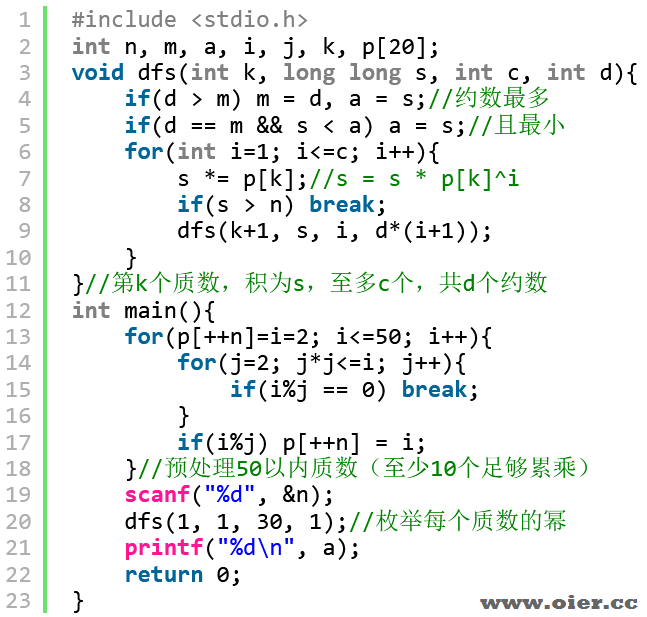
程序实现
