SSOJ2902Goldbach
4144+
作者:crxis 发布:2021-01-07 分类:筛法
题目大意:任何大于4的偶数都可以拆成两个奇素数之和,请输出质数最小的一组拆法!
题目描述
原题来自:Ulm Local,题面详见:POJ 2262
哥德巴赫猜想:任何大于 4 的偶数都可以拆成两个奇素数之和。 比如:
8=3+520=3+17=7+1342=5+37=11+31=13+29=19+23
你的任务是:验证小于 106 的数满足哥德巴赫猜想。
输入
多组数据,每组数据一个 n。
读入以 0 结束。
输出
对于每组数据,输出形如 n=a+b,其中 a,b 是奇素数。若有多组满足条件的 a,b,输出 b−a 最大的一组。
若无解,输出 Goldbach's conjecture is wrong.。
提示
样例输入
8
20
42
0样例输出
8 = 3 + 5
20 = 3 + 17
42 = 5 + 37对于全部数据,6≤n≤106。
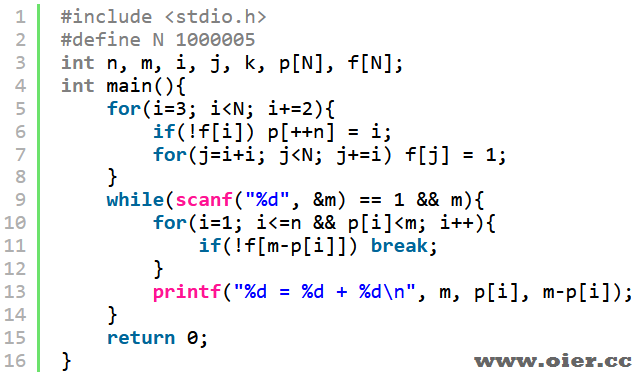
解题思路
首先用筛法筛出100万以内的质数,这样就可以用这些质数搭配,看一下是否能凑出n。枚举两个数是不可行的,可以枚举一个,看另一个是否是质数,用哈希O(1)判断不超时。
程序实现