题目大意:一个长度为n的序列,需要执行m个操作,这些操作包括区间乘一个数、区间加一个数、区间求和。
题目描述
原题来自:AHOI 2009
老师交给小可可一个维护数列的任务,现在小可可希望你来帮他完成。
你需要维护数列 $a_1, a_2, \dots, a_n$。对这个数列,有如下三种操作:
- 把数列中的一段数全部乘一个值;
- 把数列中的一段数全部加一个值;
- 询问数列中的一段数的和。由于答案可能很大,你只需输出这个数模 $P$ 的值。
输入
第一行两个整数 $n$ 和 $P$;
第二行含有 $n$ 个非负整数,从左到右依次为 $a_1, a_2, \dots, a_n$;
第三行有一个整数 $M$,表示操作总数;
接下来 $M$ 行,每行描述一个操作。题意中三种操作表示如下:
- 操作 1:
1 t g c,表示把所有满足 $t \leq i \leq g$ 的 $a_i$ 改为 $a_i \times c$; - 操作 2:
2 t g c,表示把所有满足 $t \leq i \leq g$ 的 $a_i$ 改为 $a_i + c$; - 操作 3:
3 t g,询问所有满足 $t \leq i \leq g$ 的 $a_i$ 的和模 $P$ 的值。
同一行相邻两数之间用一个空格隔开,每行开头和末尾没有多余空格。
输出
对每个操作 3,按照它在输入中出现的顺序,依次输出一行一个整数表示询问结果。
样例输入
7 43 1 2 3 4 5 6 7 5 1 2 5 5 3 2 4 2 3 7 9 3 1 3 3 4 7
样例输出
2 35 8
提示
初始时数列为 $\{1, 2, 3, 4, 5, 6, 7\}$;
经过第 1 次操作后,数列为 $\{1, 10, 15, 20, 25, 6, 7\}$;
对第 2 次操作,和为 $10 + 15 + 20 = 45$,模 $43$ 的结果是 $2$;
经过第 3 次操作后,数列为 $\{1, 10, 24, 29, 34, 15, 16\}$;
对第 4 次操作,和为 $1 + 10 + 24 = 35$,模 $43$ 的结果是 $35$;
对第 5 次操作,和为 $29 + 34 + 15 + 16 = 94$,模 $43$ 的结果是 $8$。
对于全部测试数据,$1 \leq t \leq g \leq n$,$0 \leq c, a_i \leq 10^9$,$1 \leq P \leq 10^9$。
测试数据规模如下表所示:
| 数据编号 | 1 | 2,3 | 4 | 5 | 6 | 7 | 8 | 9,10 |
|---|---|---|---|---|---|---|---|---|
| $n =$ | $10$ | $10^3$ | $10^4$ | $6 \times 10^4$ | $7 \times 10^4$ | $8 \times 10^4$ | $9 \times 10^4$ | $10^5$ |
| $M =$ | $10$ | $10^3$ | $10^4$ | $6 \times 10^4$ | $7 \times 10^4$ | $8 \times 10^4$ | $9 \times 10^4$ | $10^5$ |
解题思路
使用线段树,打多个标记即可,这里介绍矩阵做法,对于标记比较多的线段树,可以用矩阵优化思路。
一般的,我们将维护的值、答案存入一个单列的矩阵,这里需要存储区间的和。另外,一般需要存储区间的长度,这样标记下放的时候才能正确合法。
我们可以得到矩阵:
LEN
S
对于区间加x,因为S = S + x * LEN,所以我们构造矩阵:
1 0
x 1
对于矩阵乘x,因为S = S * x,我们构造矩阵:
1 0
0 x
这样,不管是加法还是乘法,我们都可以进行区间打标机或者说左乘矩阵。因为矩阵乘法满足结合律,所以不需要考虑标记的顺序了!
注意:需要预处理线段树每个结点的长度LEN,标记矩阵如果太大,可以开个u数组标记他是否有标记。
程序实现
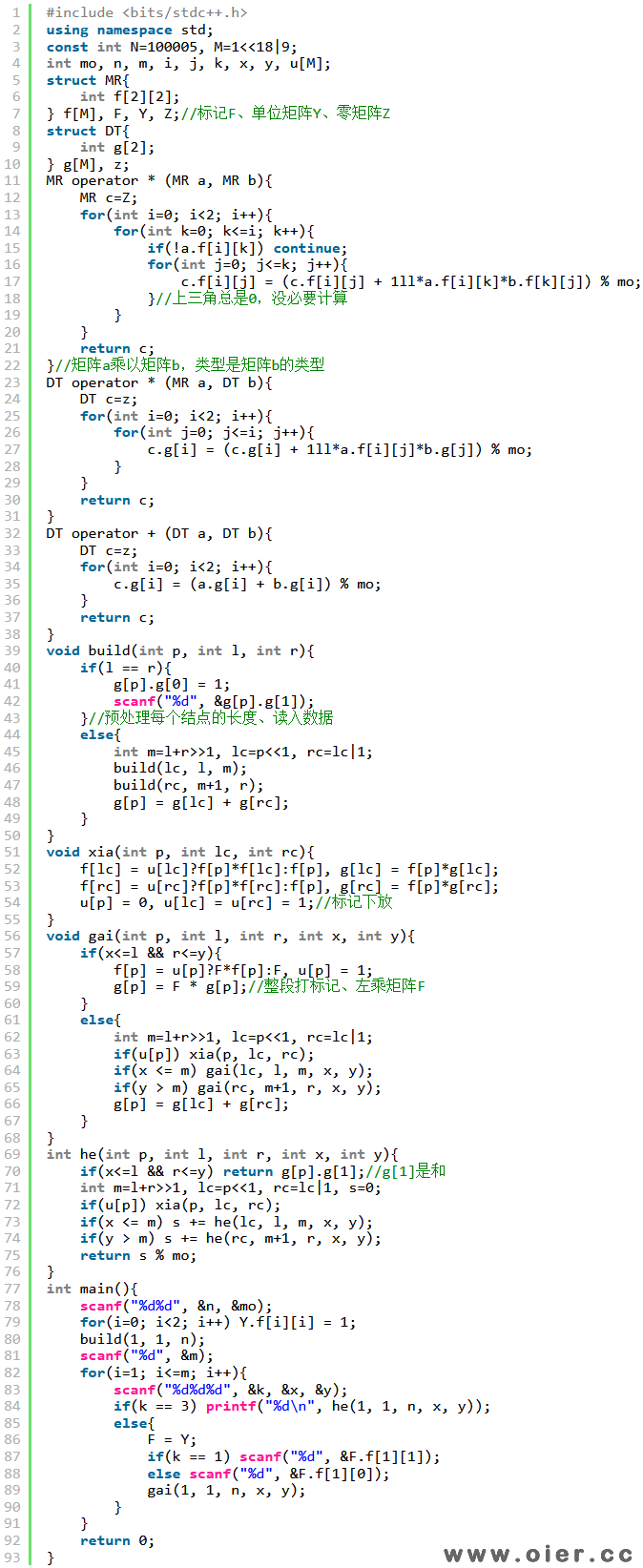
原来是这样用的 😉