SSOJ2661最大异或和
3711+
作者：crxis 发布：2018-05-15 分类：位运算
题目大意：n个正整数，你可以从中选择若干个，选取出来的数字，异或和最大是多少？
输入
输入两行，第一行一个正整数n，第二行n个正整数。
输出
输出最大异或和
样例输入
3
1 4 3
样例输出
7
提示
n在10个点的数据范围：1, 1, 3, 5, 10, 15, 20, 30, 40, 50, 50
输入的数字都是正整数，且不超过250。
解题思路
每个数字要么选，要么不选，暴力枚举，时间复杂度O(2n)，可以用搜索来写，也可以用二进制枚举：枚举1到2n -1，如枚举到5，二进制下是101，表示选其中的第1个和第3个数字出来异或。如何找出数字中的1及其位置呢？用与运算符&和左移运算符<<，如果m & (1<<3)表示数字m二进制的第4位是1……
下面介绍线性基的做法：基，就是基底的意思；通过线性基，可以表示出原来数据同样的异或值域。虽然题目要求每个数字只能选择1次，其实“选多次”也可以，因为不可能选多次！要么不选，要么选1次，选2次等于不选（异或2次抵消1^1=0），选3次跟选1次是一样的……
如果每个数字的二进制的最高位都不相同，那么只要贪心选择就行：最高位是1的那个数必选，选了就保留了最高位；如果选了的数字跟次高位不冲突，即次高位是0，必然选次高位是1的来异或出一个1……
现在，如何得到一个基底，使得每个数字的二进制最高位都不相同，而且又能表示出原来的数字能异或出的所有值呢？方法如下：
对于每一个数字，从高位往低位找1，找到后，如果对应最高位还没有记录数字，那就存到对应位；如果已经存有数字，异或一下该位数字，并继续往后找……
为什么这样就行了呢？因为这样可以保证原来的数字都能够表示出来。只要数字放下去后，异或一下前面他异或过的数字，就可以得到原来的自己；如果没有放下去，也就是说其他数字能够异或出他来。
程序实现
二进制枚举（60-70分）
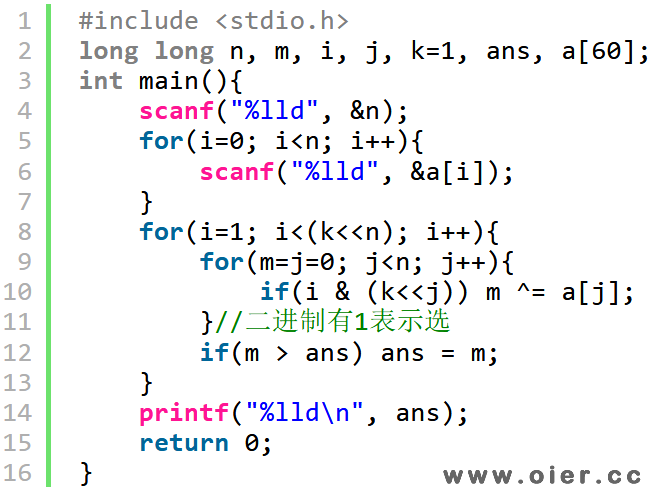
线性基（满分）
