题目大意:有n个烽火台,传递信息必须保证连续的m个至少有一个燃烧柴草,每个烽火台燃烧柴草的花费是ai,请问n个烽火台能够通信,至少花费多少?
题目描述
烽火台又称烽燧,是重要的防御设施,一般建在险要处或交通要道上。一旦有敌情发生,白天燃烧柴草,通过浓烟表达信息:夜晚燃烧干柴,以火光传递军情。在某两座城市之间有n个烽火台,每个烽火台发出信号都有一定的代价。为了使情报准确的传递,在m个烽火台中至少要有一个发出信号。现输入n、m和每个烽火台发出的信号的代价,请计算总共最少需要花费多少代价,才能使敌军来袭之时,情报能在这两座城市之间准确的传递。
输入
第一行有两个数n,m分别表示n个烽火台,在m个烽火台中至少要有一个发出信号。
第二行为n个数,表示每一个烽火台的代价(不超过100的正整数)。
输出
一个数,即最小代价。
样例输入
5 3
1 2 5 6 2
样例输出
4
提示
n和m在10个点的数据范围:5, 10, 100, 500, 1000, 5000, 10000, 30000, 50000, 70000, 100000
解题思路
f[i]表示第i个烽火台燃烧柴草,前面i个烽火台能够通信的最小花费,只要把所有的f[i]求出来,那么答案就是f[j], f[j+1], … , f[n]中的最小值,其中j=max(n-m+1, 1),因为最后一个燃烧柴草的,必须能够传递信息给n。
程序实现
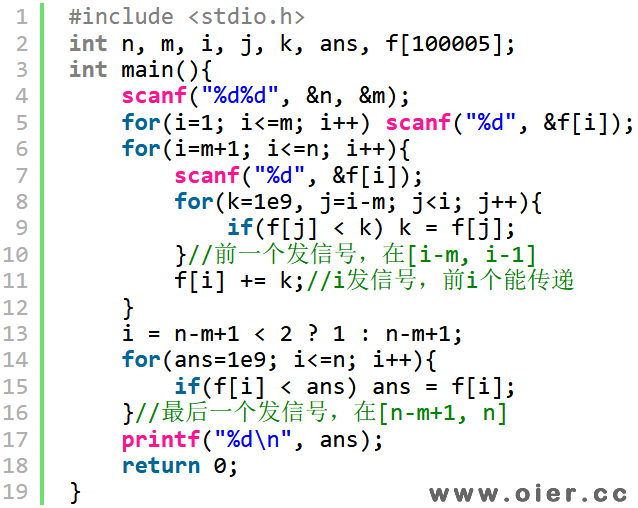
数据比较弱,暴力DP就可以过了。前面m个烽火台,f[i]=a[i]即可,因为即使前面全部不燃烧柴草也是可以的;后面的,就找前一个燃烧柴草的、总花费最小的烽火台,查找范围是i-m到i-1,注意考虑边界问题。
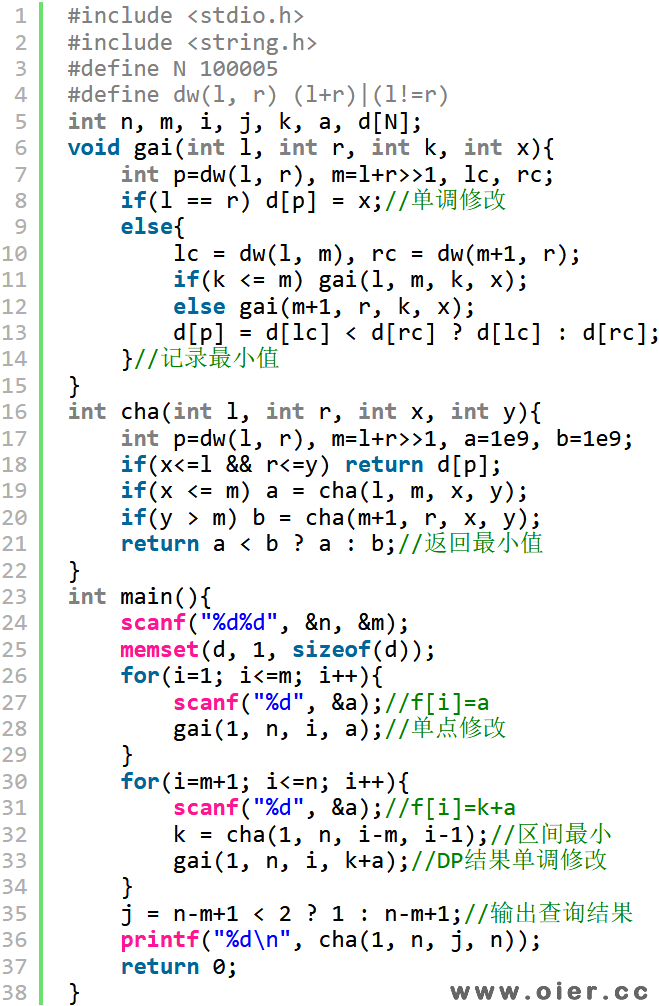
区间求最小值,可以用线段树log的复杂度查询,前面m个,f[i]=a[i],相当于单点修改;后面的,需要查询区间最小值k,然后在单点修改f[i]=k+a[i];最后输出最后一个发信号的烽火台的范围内的最小值。
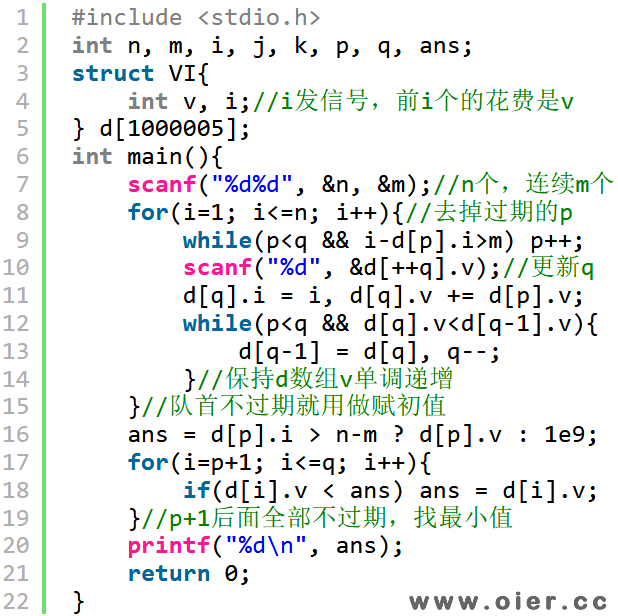
单调队列优化的DP:区间平移,寻找最值,可以用单调队列优化。f[i]在可行范围内选最小的,我们可以维护一个单调递增的队列,那么每次只需要选队头就可以了。原理:如果发现f[j]<f[j-1],那么f[j-1]就不可能用来更新后面的值了,因为能用f[j-1],肯定可以用f[j],而且f[j]更小、更优,那么肯定选f[j],永远不会选f[j-1]。因此,每进来一个f[j],我们就维护队列单调递增,见代码12-14行;当然,如果烽火台过期了,超过i的前一个烽火台的可行范围,那么这个烽火台就要从单调队列中去掉,减代码第9行;最后单调队列里面的,烽火台编号i必定是大于等于n-m的,只需要考虑队首是否满足条件,后面的直接找最小值即可。