SSOJ2628二十七进制数
5041+
作者：crxis 发布：2017-12-29 分类：字符串
题目大意：一个由小写字母组成的字符串，将他看成一个二十七进制数，其中的某一段转成十进制是多少？
题目描述
一个二十七进制数，a表示1、b表示2……z表示26，逢二十七进1，空字符是0。如aa相当于十进制下的1*27+1=28。现有一个由小写字母组成的、不超过10万位的二十七进制数，从中截取一段连续的字母出来也是一个二十七进制数，截取的这个数转成十进制后是多少？
输入
第一行两个整数n和m，表示二十七进制数的长度以及截取的次数
第二行一个长度为n的由小写字母组成的字符串
接下来m行，每行两个整数，表示截取的起始位置和终点位置
输出
对于每次截取，输出它转成的十进制数（模333333331）
样例输入
26 5
abcdefghijklmnopqrstuvwxyz
1 1
1 2
3 5
9 9
5 23
样例输出
1
29
2300
9
39375204
提示
n和m在10个点的数据范围：5, 10, 100, 500, 1000, 5000, 10000, 30000, 50000, 70000, 100000
解题思路
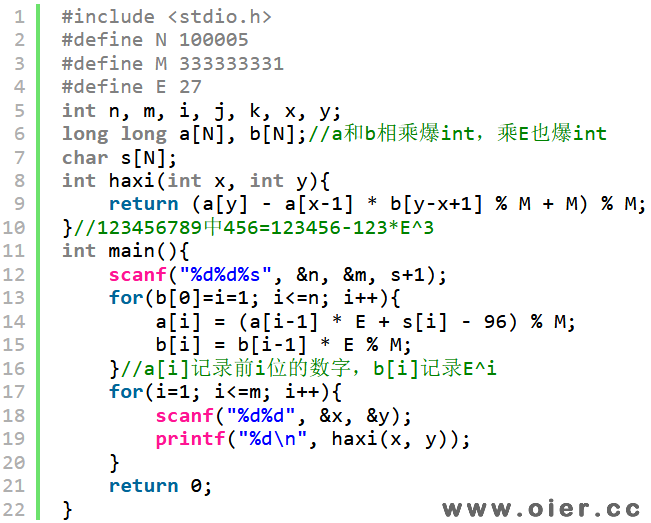
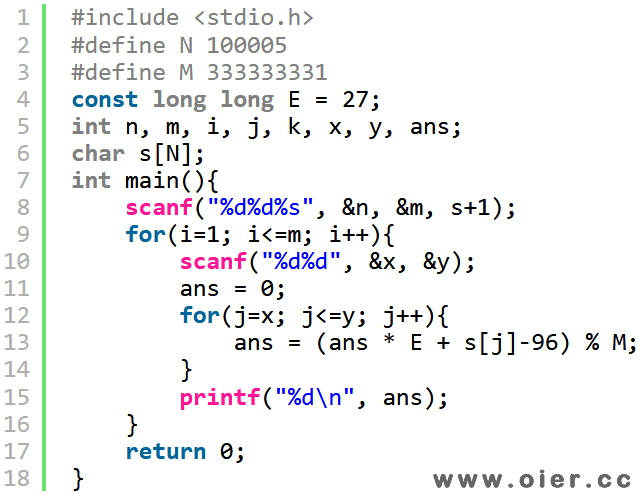
Rabin-Karp哈希，将字符串中的字符看成1、2、3……，不同字符的个数+1后可以作为基底，这样每一个字符串都可以看成一个数字，如果两个字符串转成数字后相同，那么就可以看做这两个字符串是相等的。如由26个字母组成的字符串，基底可以选27，abc可以看成是a*27*27+b*27+c。abcdefghijklmnoprstuvwxyz这样的字符串也可以转成数字。如何快速地计算中间某一段的值呢？我们可以先预处理前i个的值，如果a[i]表示前i个的值，那么第3到8个的值就是a[8]-a[2]*27^6（abcdefgh – ab******）。为了避免数字太大，我们可以模一个素数。
注意，字符看成的数字不能是0，因为如果字符a表示0，那么a和aaa的值都是0，但他们并不相等；基底的选择，必须比字符个数大，这样才能看成是一个E进制数；取模时模素数，冲突会小些。
程序实现
