题目大意:有n个数,不断地对其中的某段数字进行增减,不断地询问某一段数字的和,如何快速解决?
题目描述
给你n个整数,请问第x个到第y个的和是多少?
与上一题不同,在询问前后,这n个数中的某个区间的数可能会同时加上z。
输入
第一行:n和m,表示n个数,m个询问
第二行:n个整数
接下来m行,每行3或4个整数o、x、y(、z):o表示求和还是更改数字,如果o=1,表示第x个数到第y个数都加上z;如果o=2,表示求第x个到第y个的和。
输出
样例输入
5 3
1 2 -3 6 5
2 2 4
1 2 5 1
2 1 3
样例输出
5
2
提示
1<=x、y<=n;1<=o<=2;n个数,每个数的绝对值不超过1000;5<=n、m<=200000
(10个点数据范围:5, 10, 100, 500, 1000, 5000, 10000, 50000, 100000, 150000, 200000)
解题思路
单点修改可以用树状数组或者线段树来做,区间增减呢?区间求和是相同的,主要考虑区间增减怎么解决。
如果用线段树来做,每一个结点(线段)记录该区间的和,这样每次求区间和时间复杂度是O(log2n)。修改的话,如果每个点都修改一遍,那就是O(n)了,要整一段修改才会提高效率。要实现整段修改,就意味着如果有区间[1,5],那么如果我们需要让区间[1,5]增加3,只需要改[1,5]的值,其儿子结点全部都不改动(如果改动就是O(n)复杂度了),回溯时依次更新父亲结点记录的和。如果我需要询问区间[2,5]的和怎么办?[2,3]和[4,5]两个区间都没有增加3,我们需要记下来才行。于是,我们可以在修改[1,5]的同时,用一个数组标记其所有儿子结点还没有修改(增加3)。在求和回溯到父亲结点的时候,我们可以根据这个标记,把没有加的数加回来。需要注意的是,结点区间跟询问的区间,重合部分才需要加没加的数。
程序实现

暴力60分:

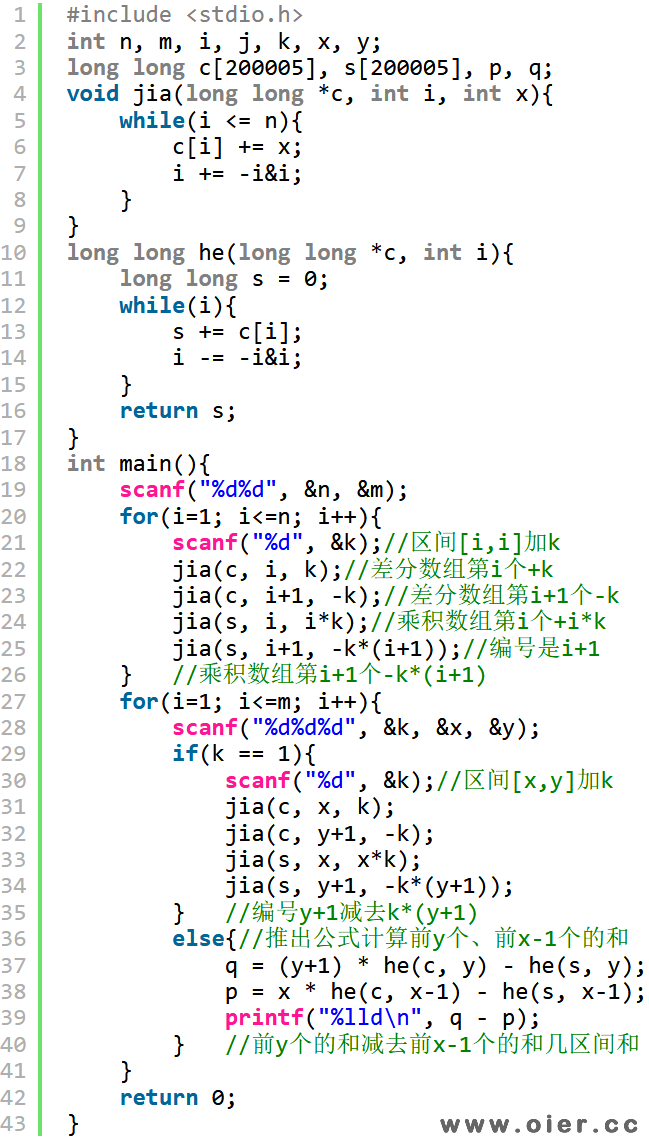
差分+树状数组:提到区间增减,不难想到差分序列。我们用a数组记录差分序列,对区间[x,y]加3,我们可以让a[x]加3,让a[y+1]减3,这样可以看成是[x,n]全部加3,[y+1,n]全部减3,也即[x,y]加3。求和时,化简一下公式即可得到树状数组的做法:如我们需要球前y个的和,数组a中下标不超过y的都会都和产生影响,如a[i]会对和产生(y-i+1)*a[i]的贡献,因为a[i]表示区间[i,n]都要加a[i],只不过现在我们求的是前y个:∑((y-i+1)*a[i]),分离参数(常数提出来)化简得(y+1)*∑a[i] + ∑(i*a[i]),也就是说我们知道差分数组前y个的和以及乘积数组前y个的和即可快速计算前y个数的和。