题目大意:有n个数,不断地对其中的某个数字进行修改,不断地询问某一段数字的和,如何快速解决?
题目描述
给你n个整数,请问第x个到第y个的和是多少?
与上一题不同,在询问前后,这n个数中的某个数可能会有改动。
输入
第一行:n和m,表示n个数,m个询问
第二行:n个整数
接下来m行,每行3个整数o、x、y:o表示求和还是更改数字,如果o=1,表示将第x个数改成y;如果o=2,表示求第x个到第y个的和。
输出
对于每次询问和,输出区间的和。
样例输入
5 3
1 2 -3 6 5
2 2 4
1 2 5
2 1 3
样例输出
5
3
提示
1<=x、y<=n;1<=o<=2;n个数,每个数的绝对值不超过1000;5<=n、m<=200000
(10个点数据范围:5, 10, 100, 500, 1000, 5000, 10000, 50000, 100000, 150000, 200000)
解题思路
读入n个数到数组a,对于每次询问,如果是修改,则直接修改a[i]的值,如果是询问区间和,值直接累加区间所有元素,时间复杂度O(m*n),不能拿满分。
程序慢在区间求和,如果用上一题的思想,记录前缀和的话,那么更新一个元素的值,还是需要O(n)更新元素后面的所有前缀和,时间复杂度并没有改变。
如何让更新元素的值时更新和比较快,而且求连续子段和也比较快呢?分块!前缀和是分成1个一块、2个一块、3个一块、……、n个一块,这样的块太多太长,更新起来比较慢。我们可以换一种方法分块:分成√n块,每块有√n个,这样更新的时候,只需要修改一块的和,时间复杂度是O(1);求和的时候,如果区间包含一整块,就直接加一整块,不是一整块就逐个加起来(非一整块的在两端,加起来不超过2*√n,中间不超过√n块),时间复杂度是O(√n)。这样总体时间复杂度就是O(m*√n)。
思考:如何判断一个元素属于哪一块?
回答:每块有p个(p=√n),元素除以p相同即同一块,这样每一块恰好p个(从0开始的话)。
求和的时候,要加√n块,√n个元素,比较耗时,能不能再快一点呢?可以,只要分块分得更加巧妙——利用二进制的思想!分块的时候,每一块都是2^k次方个(k是自然数),如果求前面y个的和,那么将长度为y的序列拆分成若干个含有2^k个元素的小块:如y=6,二进制下是110,那么拆分成5-6和1-4两块;又如y=10,二进制下是1010,那么拆分成9-10和1-8两块;又如y=15,二进制下是1111,那么拆分成15-15、13-14、9-12、1-8四块;又如32,二进制下是100000,那么拆分成1-32一块。这样,即使是一个很大的数y=123456,二进制下是1 1110 0010 0100 0000,也就分成6块,从左到右每块依次长度为2^16、2^15、2^14、2^13、2^9、2^6,求和时只需要加6次,任意一个数至多分成log2n块,也即最多加log2n次。
那么,如何记录每一小块的和呢?我们用c数组记录小块的和,c[i]表示以i结尾,连续2^k个元素的和,那么k是多少呢?
s[i]表示前i个的和,那么s[123456] = c[123456] + c[123456-2^6] + c[123456-2^6-2^9] + c[123456-2^6-2^9-2^13] + c[123456-2^6-2^9-2^13-2^14] + c[123456-2^6-2^9-2^13-2^14-2^15],再举个简单的例子,y=6,二进制下是110,那么拆分成5-6和1-4两块,s[6] = c[6] + c[6-2^1] = c[6] + c[4] = a[5]+a[6] + a[1]+a[2]+a[3]+a[4],也就是说c[6]记录的是左边离他最近的2个数的和,c[4]记录的是左边离他最近的4个数的和。那么c[i]是离他最近的几个数的和?最右边的那个1!c[6]之所以表示最近的2个,是因为110分成100和10两块,10是接近6的那一块;c[123456]之所以表示最近的2^6个,是因为1 1110 0010 0100 0000分成1 0000 0000 0000 0000、1000 0000 0000 0000、100 0000 0000 0000、10 0000 0000 0000、10 0000 0000、100 0000共6块,100 0000是接近123456的那一块。加了y最右边那一块之后,那么还需要求前面y-2^k个的和,即求前面那些小块的和。如果是6的话,那么要从c[6]跳到c[4](因为已经加了2个的和了,所有6-2=4)。
求和的问题解决了,c[i]表示什么也确定了,那么更新的时候如何更新呢?如我要更新a[1],那么含有a[1]的块有哪些?也就是需要更新和的块有哪些?二进制下,1的二进制是1,被1、10、100、1000等包含(101仅包含101这个元素、110近包含110和101两个元素),故需要更新c[1]、c[2]、c[4]、c[8]……那么更新a[5]呢?5的二进制是101,被101、110、1000、10000等包含(110包含110和101两个元素),故需要更新c[5]、c[6]、c[8]、c[16]……不难发现,1、2、4、8以及5、6、8、16的变化规律就是前一个数加上最右边的那个1,因为这个1管的就是自己前面2^k次方个元素的和。
读入数据以及修改数据的时候,更新包含该元素的块的和;求和区间[x, y]的和的时候,用前y个的和减去前x-1个的和即可,时间复杂度O(m*log2n)。
程序实现
树状数组O(mlog2n):

分块O(m√n):

暴力70分O(mn):

===================线段树做法===================
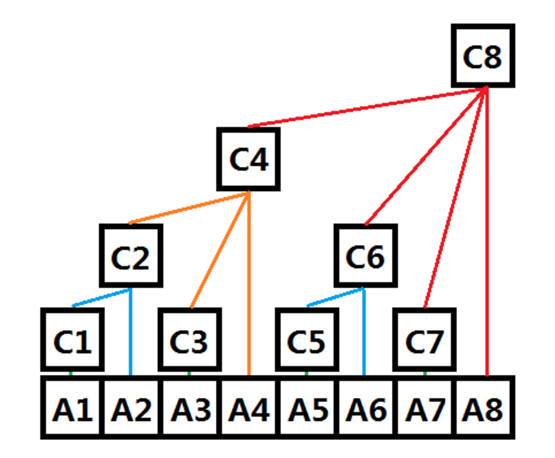
结构体存储,记录区间端点、左右儿子、线段和:

不难发现,在递归的过程中,区间端点是可以算出来的,不需要记录:
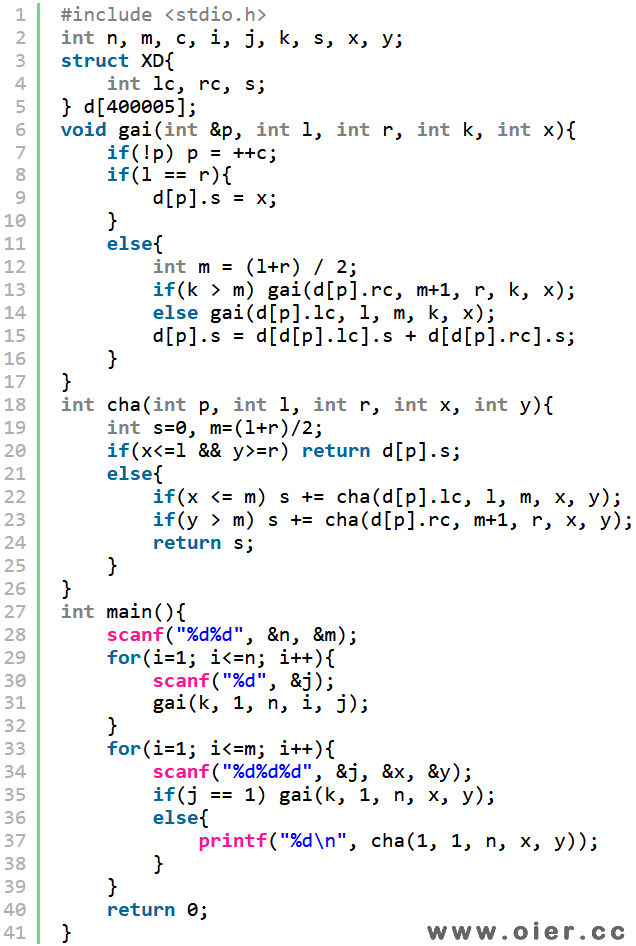
堆结构存储,不需要记录左右儿子是谁,结点p的左儿子是p*2,右儿子是p*2+1,数组大小1<<⌈log2n⌉+1,具体请看下一篇文章:
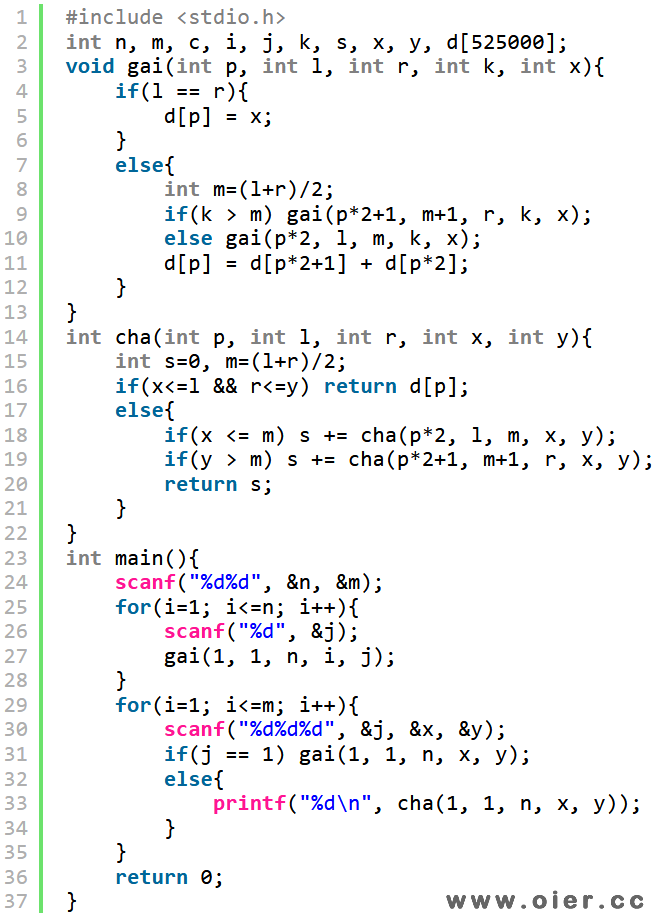
堆结构存储,最后一层可能空很多,浪费空间,可以使用更紧凑的存储方式:叶子节点分别存在编号为2、4、6、……、2n位置,父亲结点存储在儿子结点的中间位置,如果是偶数就+1变成奇数,达到每个结点都有自己的固定位置,区间[l,r]的位置计算方法:(l+r)|(l!=r),非叶子结点|1总会是奇数。
