题目描述

有一个m × m的棋盘，棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。

任何一个时刻，你所站在的位置必须是有颜色的（不能是无色的）， 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时，如果两个格子的颜色相同，那你不需要花费金币；如果不同，则你需要花费 1 个金币。

另外， 你可以花费 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用， 而且这个魔法的持续时间很短，也就是说，如果你使用了这个魔法，走到了这个暂时有颜色的格子上，你就不能继续使用魔法； 只有当你离开这个位置，走到一个本来就有颜色的格子上的时候，你才能继续使用这个魔法，而当你离开了这个位置（施展魔法使得变为有颜色的格子）时，这个格子恢复为无色。

现在你要从棋盘的最左上角，走到棋盘的最右下角，求花费的最少金币是多少？

输入输出格式

输入格式：

数据的第一行包含两个正整数 m， n，以一个空格分开，分别代表棋盘的大小，棋盘上有颜色的格子的数量。

接下来的 n 行，每行三个正整数 x， y， c， 分别表示坐标为（ x， y）的格子有颜色 c。

其中 c=1 代表黄色， c=0 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为（ 1, 1），右下角的坐标为（ m, m）。

棋盘上其余的格子都是无色。保证棋盘的左上角，也就是（ 1， 1） 一定是有颜色的。

输出格式：

输出一行，一个整数，表示花费的金币的最小值，如果无法到达，输出-1。

输入输出样例

5 7
1 1 0
1 2 0
2 2 1
3 3 1
3 4 0
4 4 1
5 5 0

8

5 5
1 1 0
1 2 0
2 2 1
3 3 1
5 5 0

-1

说明

输入输出样例 1 说明

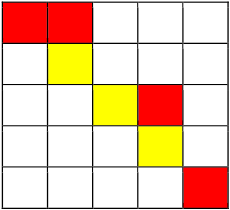
从（ 1， 1）开始，走到（ 1， 2）不花费金币

从（ 1， 2）向下走到（ 2， 2）花费 1 枚金币

从（ 2， 2）施展魔法，将（ 2， 3）变为黄色，花费 2 枚金币

从（ 2， 2）走到（ 2， 3）不花费金币

从（ 2， 3）走到（ 3， 3）不花费金币

从（ 3， 3）走到（ 3， 4）花费 1 枚金币

从（ 3， 4）走到（ 4， 4）花费 1 枚金币

从（ 4， 4）施展魔法，将（ 4， 5）变为黄色，花费 2 枚金币，

从（ 4， 4）走到（ 4， 5）不花费金币

从（ 4， 5）走到（ 5， 5）花费 1 枚金币

共花费 8 枚金币。

输入输出样例 2 说明

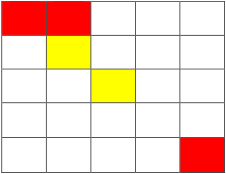
从（ 1， 1）走到（ 1， 2），不花费金币

从（ 1， 2）走到（ 2， 2），花费 1 金币

施展魔法将（ 2， 3）变为黄色，并从（ 2， 2）走到（ 2， 3）花费 2 金币

从（ 2， 3）走到（ 3， 3）不花费金币

从（ 3， 3）只能施展魔法到达（ 3， 2），（ 2， 3），（ 3， 4），（ 4， 3）

而从以上四点均无法到达（ 5， 5），故无法到达终点，输出－1

数据规模与约定

对于 30%的数据， 1 ≤ m ≤ 5， 1 ≤ n ≤ 10。

对于 60%的数据， 1 ≤ m ≤ 20， 1 ≤ n ≤ 200。

对于 100%的数据， 1 ≤ m ≤ 100， 1 ≤ n ≤ 1,000。