OIer博客

题目描述

Sylvia 是一个热爱学习的女♂孩子。

前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。

Sylvia 所在的方阵中有$n\times m$名学生，方阵的行数为 $n$，列数为 $m$。

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中 的学生从 1 到 $n\times m$ 编上了号码（参见后面的样例）。即：初始时，第 $i$ 行第 $j$ 列 的学生的编号是$(i-1)\times m+j$。

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天 中，一共发生了 $q$件这样的离队事件。每一次离队事件可以用数对$(x,y)(1\le x\le n,1\le y\le m)$描述，表示第 $x$ 行第 $y$ 列的学生离队。

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达 这样的两条指令：

1. 向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条 指令之后，空位在第 $x$ 行第 $m$ 列。
2. 向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条 指令之后，空位在第 $n$ 行第 $m$ 列。

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后， 下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 $n$ 行 第 $m$ 列一个空位，这时这个学生会自然地填补到这个位置。

因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学 的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后 方阵中同学的编号可能是乱序的。

输入输出格式

输入格式：
输入共 $q+1$ 行。

第 1 行包含 3 个用空格分隔的正整数 $n,m,q$，表示方阵大小是 $n$ 行 $m$ 列，一共发 生了 $q$ 次事件。

接下来 $q$ 行按照事件发生顺序描述了 $q$ 件事件。每一行是两个整数 $x,y$，用一个空 格分隔，表示这个离队事件中离队的学生当时排在第 $x$ 行第 $y$ 列。

输出格式：
按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学 生的编号。

输入输出样例

2 2 3 
1 1 
2 2 
1 2

1
1
4

说明

【输入输出样例 1 说明】

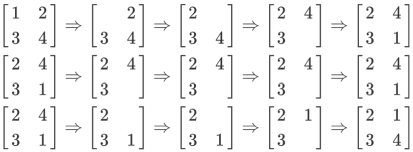
列队的过程如上图所示，每一行描述了一个事件。 在第一个事件中，编号为 1 的同学离队，这时空位在第一行第一列。接着所有同学 向左标齐，这时编号为 2 的同学向左移动一步，空位移动到第一行第二列。然后所有同 学向上标齐，这时编号为 4 的同学向上一步，这时空位移动到第二行第二列。最后编号 为 1 的同学返回填补到空位中。

【数据规模与约定】

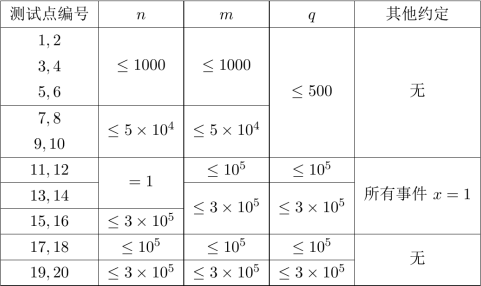
数据保证每一个事件满足 $1\le x\le n,1\le y\le m$