题目大意:从n个点m条边,从x点到其他各个点的最短距离是多少?
题目描述
现在,有一个好人在城市x坐地铁,请问从城市x到其他城市,分别需要花费多少个S币?
(注意:不能到达的城市,不需要任何费用,即费用为0;两个城市之间可以有多条直接相连的地铁,且费用不一样。)
输入
接下来m行,每行3个整数a、b、c,表示城市a到城市b的路程是c公里
输出
样例输入
6 5 1
1 2 5
2 3 8
1 4 2
4 5 2
5 3 2
样例输出
0
5
6
2
4
0
提示
5 <= n <= 10000
10 <= m <= 100000
1 <= a、b <= n
1 <= c <= 100
60%的数据:n <= 5000
80%的数据:n <= 8000
解题思路
用迪杰斯特拉算法怎么AC?先考虑60分!60%的数据n不超过5000,用迪杰斯特拉可以过;对于80%的数据,时间应该可以接受,就是空间超过128M内存了,可以考虑二维数组开short;对于100%的数据,时间应该到达极限了,空间用char还可以接受!
如果怕超时,可以用优先队列找最短距离的点,更新到其他点的最短距离时,可以扫一下该点能到的下一个点,用前向星就会快很多了。由于共有m条边,每条边至多让一个点入队,因此队列点数不超过m,时间复杂度在O(mlog2m)范围内,由于只有确定最短路径的点才会扫边,因此每条边只会扫一次。
程序实现
60分程序,开5000*5000数组,不会爆内存:

80分程序,开8000*8000的short数组,也不会爆内存:

100分迪杰斯特拉程序,开10000*10000的char数组,不会爆内存,要想不超时,第25行的条件需要注意了:(mp[k][j] && s[k]+mp[k][j] < s[j])不会超时,如果写成(!u[j] && mp[k][j] && s[k]+mp[k][j] < s[j])或者(s[k]+mp[k][j] < s[j] && mp[k][j])则有可能过不了第10个点,为什么?想想就知道了!

如何优化时间?找最近那个点时用优先队列,每次查找的复杂度有O(n)编程O(log2n),另外,堆/优先队列中的结点不好修改信息,同一个点可能重复入队,为了让每一条边只能访问一次,不是最近的点就不用更新距离了;为了避免n方复杂度,边可以采用前向星、邻接表等来存储。下面是结构体数组存储边,排序得到前向星:
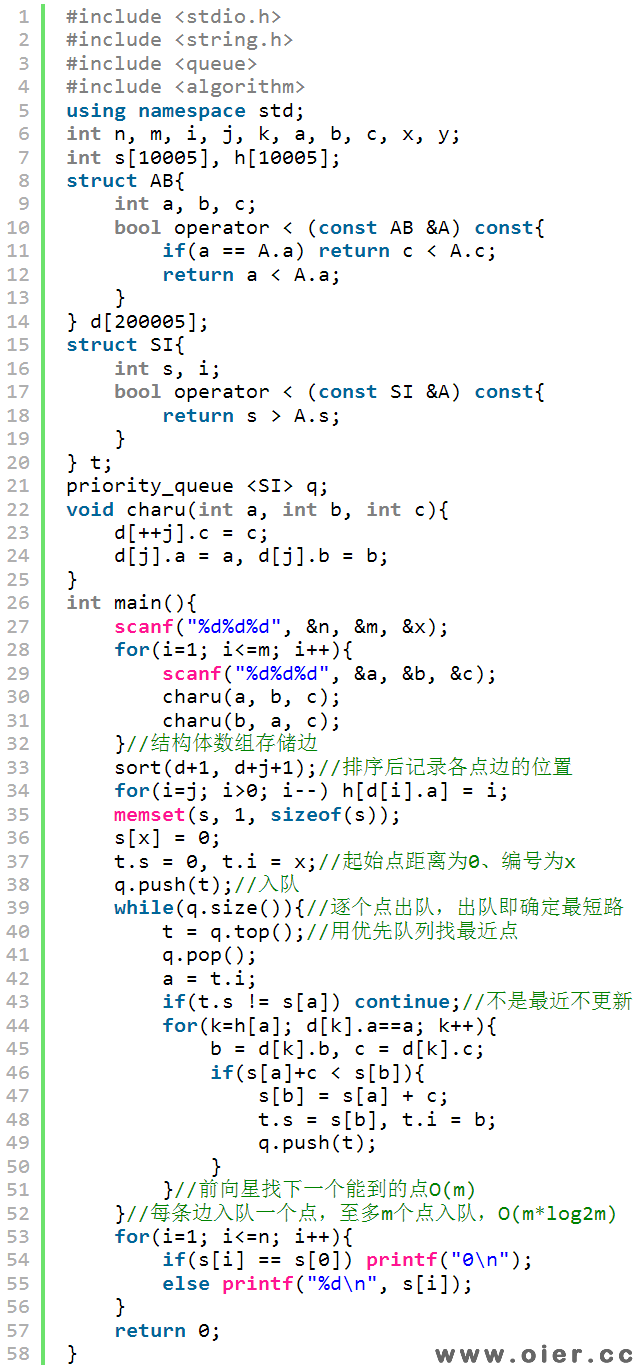
快排复杂度比较高,可以用桶排,将结构体数组划分出n个区域,第i个区域存放第i个点的边:
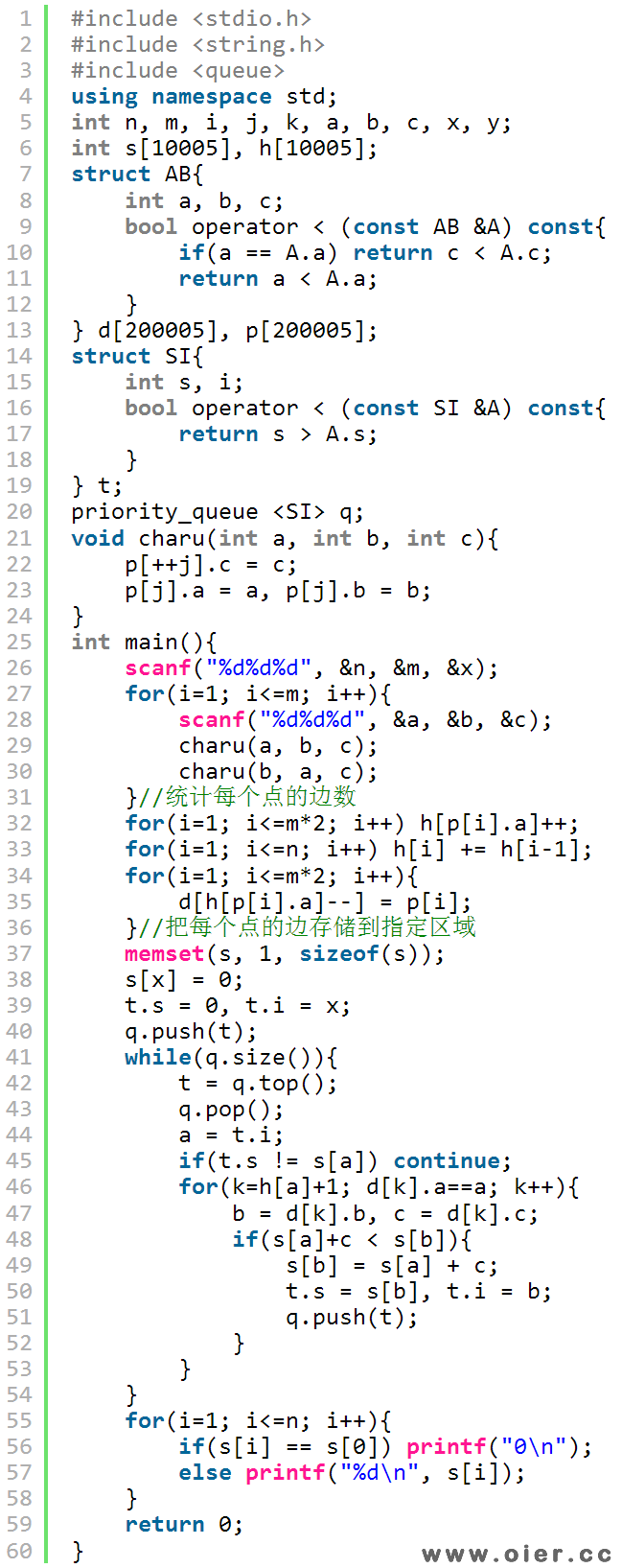
用邻接表存储,不需要排序就可以快速得到某个点的边:
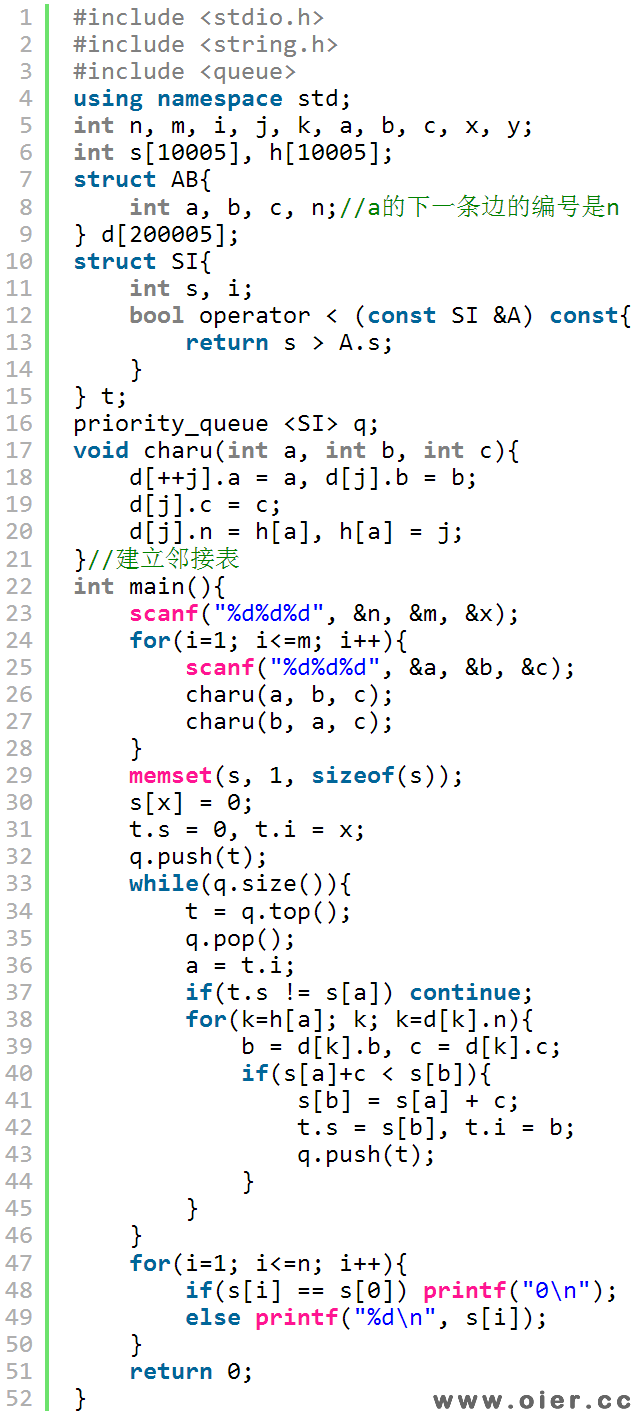
用广搜求最短路径,就跟迷宫找最少步数差不多,只是可能出现更近的点,需要重复入队;为了避免无意义重复入队,用u数组记录该点是否在队列中,在的话就不需要再入队了,这就是SPFA:
