题目大意:N个妹子要喝水,每个妹子用水杯喝水的时间从A时刻开始到B时刻结束,最少需要多少个水杯?
输入
输入第一行一个数 N,接下来 N 行每行一对数 (A,B)。
输出
输出一行一个数表示答案。
样例输入
5
1 10
2 4
3 6
5 8
4 7
样例输出
4
提示
对于 10% 的数据,有 1 ≤ N ≤ 10
对于 100% 的数据,有 1 ≤ N ≤ 2000000, 0 ≤ A,B ≤ 15000000
本题输入文件不超过 35M,建议开启输入优化。
解题思路
记录各个时间点开始喝水的人数x[i]、喝完水的人数y[i],遍历所有时间点,如果当前时间是i,那么喝水的人数在原来基础上加上这个时间点开始喝水的人数,再减去上一个时间点喝完水的人数。这样,每个时间点喝水的人数,就是前面所有开始喝水的人数减去前面所有喝完水的人数了。
下面讲一下差分如何实现。
首先,介绍一下差分序列:如果原来的数据是a[1],a[2],a[3],a[4],a[5],..,a[n],差分序列是c[1],c[2],c[3],c[4],c[5],..,c[n],那么c[1]=a[1],c[2]=a[2]-a[1],c[3]=a[3]-a[2],…,c[n]=c[n]-c[n-1]。
接着,我们看一下差分序列的特点:c[1]+c[2]+c[3]+…+c[k] = c[1] + c[2-c[1] + c[3]-c[2] + … + c[k]-c[k-1] = a[k],也就是说c[i]的前k项和救赎a[k]。
下面,我们看一下差分序列的区间修改:就用这道题来说,a时刻开始喝水,b时刻喝完水,如果我们用一个f数组记录各个时间点的喝水人数,那么f[a]…f[b]这一段都需要+1,标记一次的时间复杂度是O(B),B是15000000哦!如果用差分数组的话,就只需要O(1)的时间复杂度,我们我们看c数组,c[i] = f[i] – f[i-1]。c数组中发生改变的只有2个元素——c[a]和c[b+1],因为相邻两项相减,其他两两相邻的要么都不加,要么都加相同大小,即不变。记录好差分数组后,我们想要求f[i],只需要求c[i]的前缀和就行。
程序实现
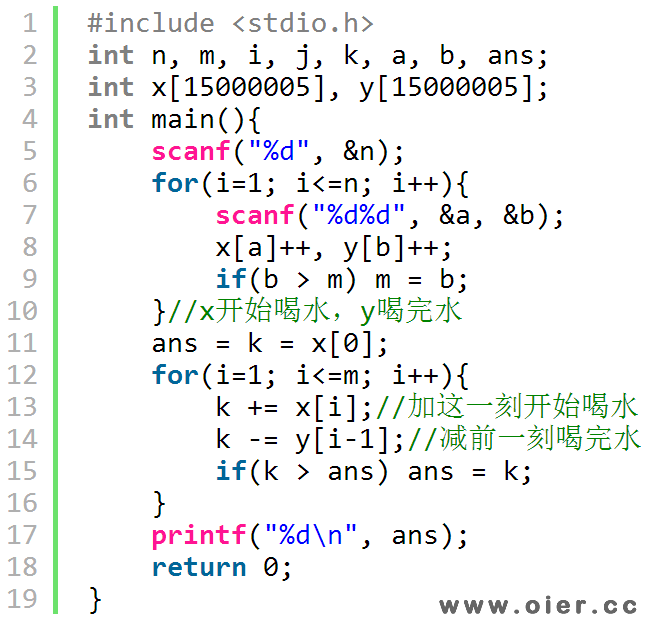
差分序列代码实现:
