题目大意:发奖金,每个人至少发100元,而且知道某人比某人奖金多,请问至少发多少奖金?
题目描述
由于无敌的凡凡在2005年世界英俊帅气男总决选中胜出,Yali Company总经理Mr.Z心情好,决定给每位员工发奖金。公司决定以每个人本年在公司贡献为标准来计算他们得到的奖金是多少。
于是Mr.Z下令召开m方会谈。每位参加会谈的代表提出了自己的意见:“我认为员工a的奖金应该比b高!”Mr.Z决定要找出一种奖金方案,满足各位代表的意见,且同时使得总奖金数最少。每位员工奖金最少为100元。
输入
第1行:两个整数n、m,表示员工总数和代表数;
以下m行:每行2个整数a,b,表示某个代表认为第a号员工奖金应该比第b号员工高,两个数之间用一个空格隔开。
输出
若无法找到合理方案,则输出“Poor Xed”;否则输出一个数表示最少总奖金。
样例输入
2 1
1 2
样例输出
201
提示
数据范围:
80%的数据满足:n<=1000,m<=2000;
100%的数据满足:n<=10000,m<=20000。
解题思路
a奖金比b多,建立一条b→a的有向边。首先考虑特殊情况,如果出现一个环(正环),如出现a的奖金比b多且b的奖金比a多,那么两个人(这一圈人)的奖金肯定越来越多,即没有合理方案。
除去特殊情况,肯定有人的奖金是100元,因为至少100元,这些人就是入度为0的点,题目不比其他人奖金多。先把这些入度为0的点入队,并设奖金为100,然后依次出队,弧头的奖金至少比弧尾的奖金多1,即f[b] = max(f[b], f[a]+1)。由于没有正环,程序结束后,每个人的奖金都求出来了。
如果出现环,那么在环里面的人肯定没有入队列,即队列长度小于n。最后我们可以根据队列长度判断是否“Poor Xed”。
程序实现

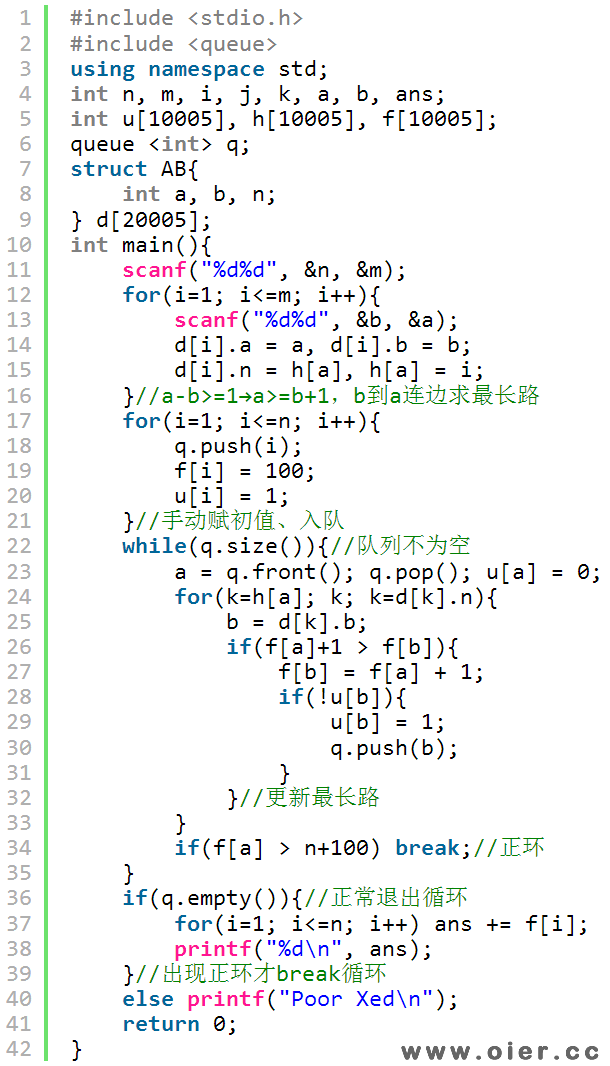
下面是差分约束系统的做法:a-b>=1即a>=b+1,转换成求最长路的边是b→a权值为1,如果不出现正环,求最长路能正常结束,此时必定满足所有“a-b>=1”的不等式;如果出现正环,某些人的奖金肯定越来越多,但我们知道,一个人的奖金不可能超过n+100,因为一个比一个多奖金也就是n+99,所以一旦出现奖金太高(n+100),即可判断出现正环,即没有合理方案。(a-b>=1也可以转成b<=a-1,建立a→b权值为-1的有向边,然后求最短路,如果出现负环就没有合理方案)