题目大意:n颗珍珠,先知道某些珍珠比某些珍珠重,请问有多少颗珍珠不可能是中间重量?
题目描述
有n颗形状和大小都一致的珍珠,它们的重量都不相同。n为整数,所有的珍珠从1到n编号。你的任务是发现哪颗珍珠的重量刚好处于中间,即在所有珍珠的重量重,该珍珠的重量列(n+1)/2位。下面给出将一对珍珠进行比较的办法:
给你一架天平用来比较珍珠的重量,我们可以比出两个珍珠哪个更重一些,在作出一系列的比较后,我们可以将某些肯定不具备中间重量的珍珠拿走。
例如,下列给出对5颗珍珠进行四次比较的情况:
(1)珍珠2比珍珠1重
(2)珍珠4比珍珠3重
(3)珍珠5比珍珠1重
(4)珍珠4比珍珠2重
根据以上结果,虽然我们不能精确地找出哪个珍珠具有中间重量,但我们可以肯定珍珠1和珍珠4不可能具有中间重量,因为珍珠2、4、5比珍珠1重,而珍珠1、2、3比珍珠4轻,所以我们可以移走这两颗珍珠。
写一个程序统计出共有多少颗珍珠肯定不会是中间重量。
输入
第一行:包含两个用空格隔开的整数N和M,其中1<=N<=99,且N为奇数,M表示对珍珠进行的比较次数
接下来M行每行包括两个用空格隔开的整数x和y,表示珍珠x比珍珠y重,两个数之间用空格隔开
输出
一行包括一个整数,表示不可能是中间重量的珍珠的总数
样例输入
5 4
2 1
4 3
5 1
4 2
样例输出
2
解题思路
如何判断一颗珍珠不可能是中间重量?如果有过半(超过n/2)的珍珠比他轻或者过半(>n/2)珍珠比他重,那么他就不可能是中间的。建图,a比b中则建立一条a到b的有向边:对于每颗珍珠,遍历一下他能到的点,点的个数就是比他轻的珍珠的个数;同样地,建立方向边后也遍历一下,就知道比他重的珍珠的个数。遍历既可以深度优先遍历,也可以广度优先遍历,访问过的点标记访问过,不再访问它,这样每次遍历的复杂度是O(m+n),整体复杂度是O(m*n+n*n)。
当然,也可以用弗洛伊德(Floyd)算法,二维数组原来是记录a到b的距离的,现在我们只需要记录a是否能到b而已,5行跑完后,就知道n个点之间的轻重情况了,这样也就可以快速统计比某个点重或者轻的珍珠个数。
程序实现
深搜
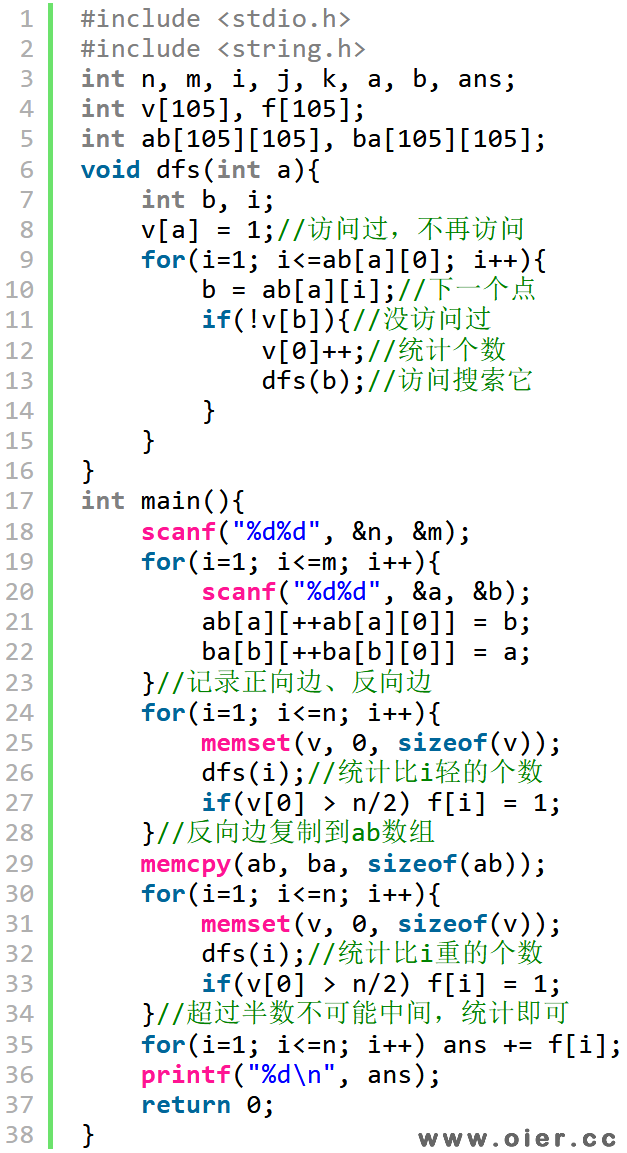
广搜
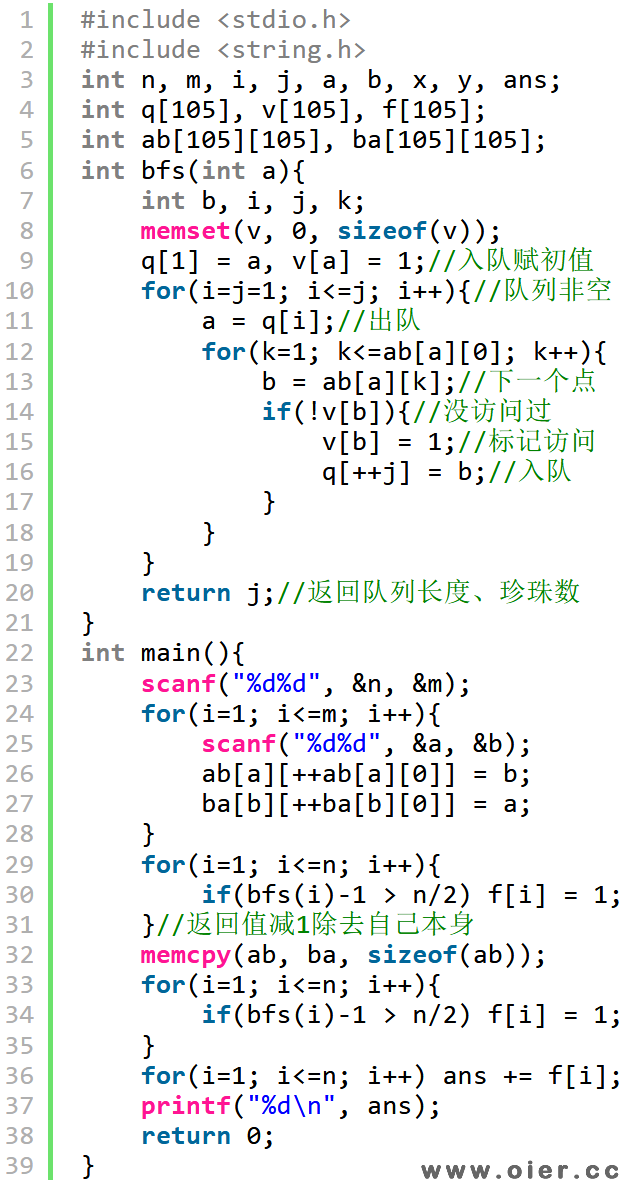
Floyd
