SSOJ2413友好城市
2998+
作者：crxis 发布：2017-10-26 分类：序列DP
题目大意：大河两岸，各有n个城市，两边城市坐标范围在1到10000，每个城市都有自己独特的友好城市，友好城市需要连航线，怎么连接航线最多？
题目描述
Palmia国有一条横贯东西的大河，和有笔直的南北两岸，岸上有位置各不相同的N个城市。北岸的每个城市有且仅有一个友好城市在南岸，而且不同城市的友好城市不同。每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市，但是由于河上雾太大，政府决定避免任意两条航道交叉，以避免事故。编程帮助政府做出一些批准和拒绝申请的决定，使得在保证任意两条航线不相交的情况下，被批准的申请尽量多。
输入
第1行，一个整数N（1<=N<=5000）,表示城市数。
第2行到第n+1行，每行两个整数，中间用1个空格隔开，分别表示南岸和北岸的一对友好城市的坐标。（0<=xi<=10000）
输出
仅1行，输出一个整数，表示政府所能批准的最多申请数。
样例输入
7
22 4
2 6
10 3
15 12
9 8
17 17
4 2
样例输出
4
解题思路
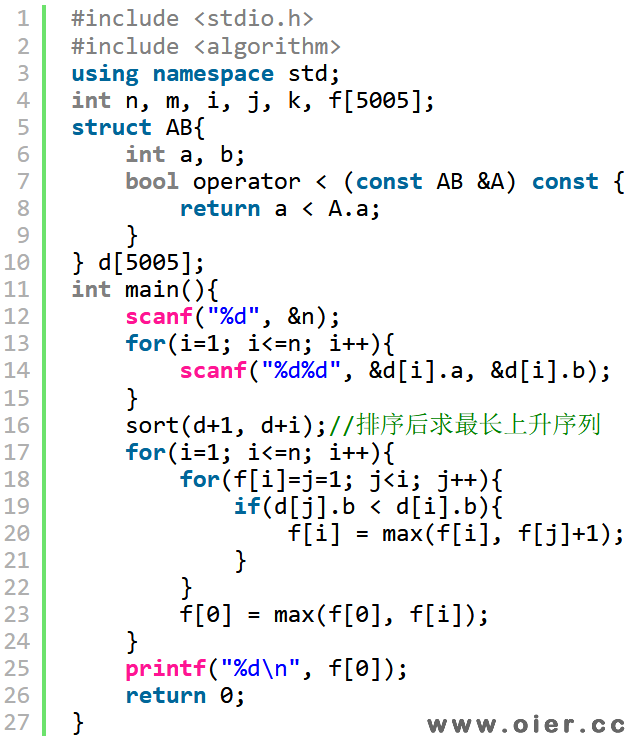
转成最长上升子序列来做就行：按河的一边的坐标来从小到大排序，这样，他们对应的友好程序的坐标是一个序列，要想让航线不交叉，那么开通的航线对应的坐标就只能递增！
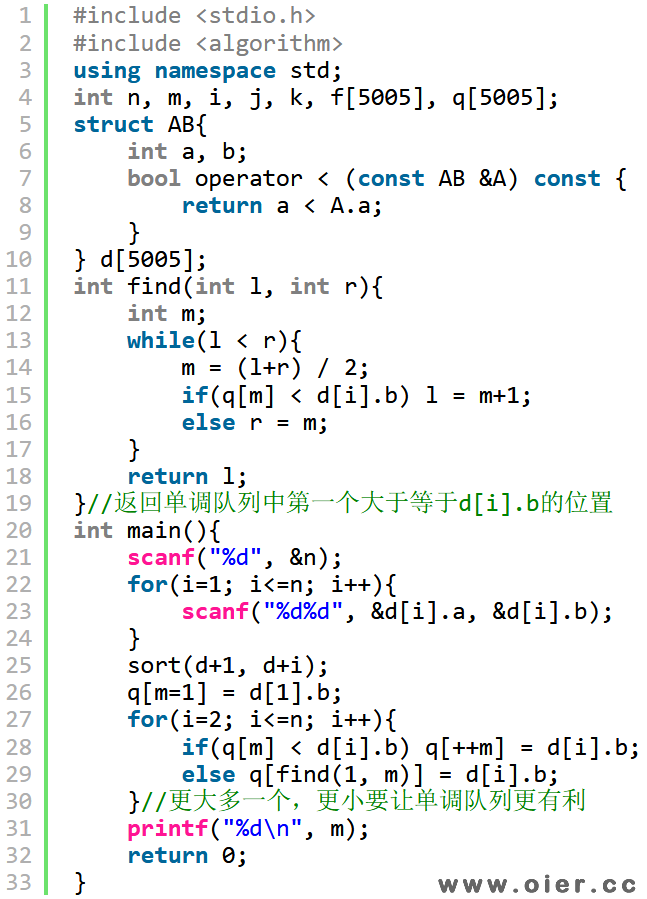
下面介绍一下如何用二分单调队列来求最长上升子序列。第一个数先入队，后面的数依次这样入队：如果他比队列中最大的还大，那么直接放到队尾，这样上升序列会更长；如果他不是最大的，那么在队里中找最接近他的比他大的数，用他去代替那个数。这样的队列是一个单调队列，可以用二分快速找到合适的位置进行更新操作。为什么可行呢？因为我们不需要考虑最后的序列是怎样的，换一个数字后，最长上升子序列长度并没有改变，如果那个位置是i，那么改变的只是让长度为i的那个上升子序列的最后一个元素变小了而已，这样对序列边长更加有利，而且不影响最终的长度。
程序实现
