SSOJ2412完全背包
5219+
作者:crxis 发布:2017-10-25 分类:01背包
题目大意:n种物品放到一个载重量为m的背包,每种物品可以选多次,最多能装多大价值的物品?
题目描述
设有n 种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限的,同时有一个背包,最大载重量为m,今从n 种物品中选取若干件(同一种物品可以多次选取),使其重量的和小于等于m,而价值的和为最大。
输入
第1行:两个整数,m(背包容量,m<=200)和n(物品数量,n<=30);
第2至n+1行:每行两个整数Wi,Ci,表示每个物品的重量和价值。
输出
仅一行,一个数,表示最大总价值。
样例输入
10 4
2 1
3 3
4 5
7 9
样例输出
max=12
解题思路
可以转成01背包来做:虽然每种物品可以选无限次,但总会有一个上限,如第一种物品,最多只能选m/wi次,再多就装不下了,时间复杂度O(m*∑(m/wi))。
由于容量可能很大,物品重量可能很小,这样物品数量就极大,可能远远超过n,造成超时。因此,我们可以采取更巧妙的方法,从小到大枚举容量(重量),如一个物品重量是2,那么求f[2]的时候用到f[0],求f[3]的时候用到f[1],求f[4]的时候用到f[2]……因为f[2]已经装过一次这个物品了,f[4]再装一次,相当于2次,如果后面又用到f[4],那么就是“多次选”、“无限次”了。
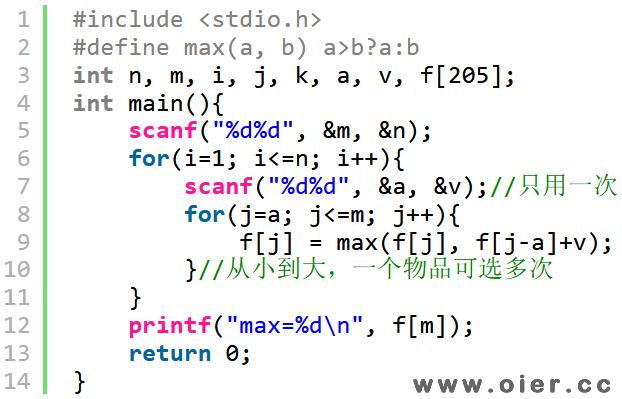
程序实现