题目大意:m个单位时间,n种药,现告诉你每种药的价值以及采药花费的时间,请问最多能采到多大价值?
题目描述
辰辰是天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。因此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里给他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入
第1行有两个整数T(1<=T<=1000)和M(1<=M<=100),用一个空格隔开,T代表总共能够用来采药的时间,M代表山洞里的草药的数目。接下来的M行每行包括两个1到100之间(包括1和100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出
1行,只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
样例输入
70 3
71 100
69 1
1 2
样例输出
3
提示
30%的数据满足:M<=10;
100%的数据满足:M<=100.
解题思路
n种药,第i种药的价值是vi,花费时间是ai,共有m个单位的时间。如果只有1种药,那很好办,时间够就采到,可以增加价值,否则采不到,价值为0;2种药呢?第1种可以按照原计划,第2种就不行了,因为m个单位的时间,可能有部分时间采了其他药。
会变化的是药的数量以及时间,我们可以定义状态f[i][j]表示前面i种药花费j个单位的时间能获得的最大价值,那么f[i][j] = max(f[i-1][j], f[i-1][j-ai] + vi),其中前者是第i种药不采,价值等于前面i-1种药的最大价值,后者是采第i种药,价值是第i种药的价值加上前面i-1种药同等时间减去这种药需要花费的时间。
程序实现
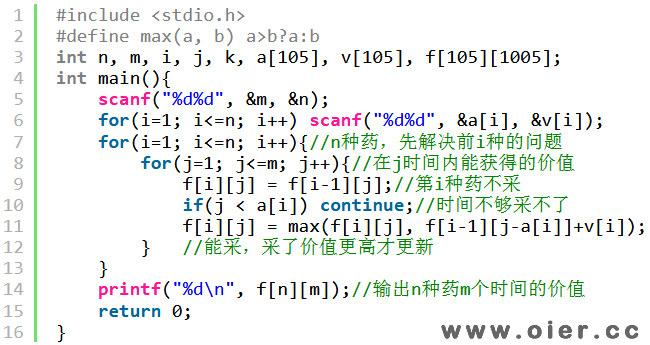
滚动数组可以减少空间的使用,因为求f[i][j],时候用到数组f[i-1][],因此当i是奇数的时候,用f[1]来存储,借助“上次”的数据f[0]来计算;当i是偶数的时候,用f[0]来存储,借助“上次”的数据f[1]来计算。正整数下i&1可以看作是i%2,位运算速度更快;异或1可以让1变为0,让0变为1。
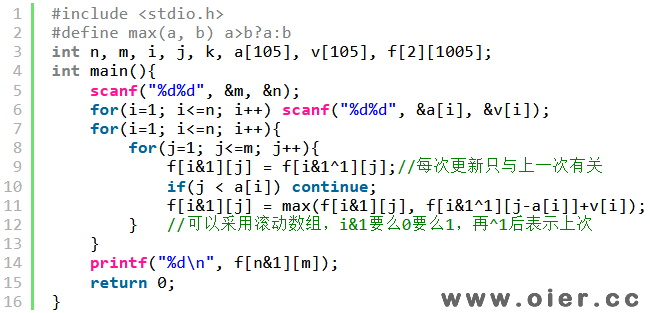
不难发现,如果第i种药不采,那么上一次的数据需要复制到这一次的数据中,能不能用同一个数组,这样就不需要浪费时间复制了?可以的,但需要倒着来,计算f[j]的时候,会用到f[j-ai],因此,要先计算f[j-ai],再计算f[j],这样就保证了f[j]用的是上一次的数据,而不是这次更新后的数据。

提示:如果从小到大计算f[j],那么一种药可以采多次。