题目大意:两个字符串,各自按照原来顺序依次抽出字符,最长的公共子序列是多长?
题目描述
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说,若给定序列X= { x1, x2,…, xm},则另一序列Z= {z1, z2,…, zk}是X的子序列是指存在一个严格递增的下标序列 {i1, i2,…, ik},使得对于所有j=1,2,…,k有 Xij=Zj。
例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。给定两个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。例如,若X= { A, B, C, B, D, A, B}和Y= {B, D, C, A, B, A},则序列{B,C,A}是X和Y的一个公共子序列,序列{B,C,B,A}也是X和Y的一个公共子序列。而且,后者是X和Y的一个最长公共子序列,因为X和Y没有长度大于4的公共子序列。给定两个序列X= {x1, x2, …, xm}和Y= {y1, y2, … , yn},要求找出X和Y的一个最长公共子序列。
输入
输入共两行。每行为一个由大写字母构成的长度不超过200的字符串,表示序列X和Y。
输出
输出第一行为一个非负整数。表示所求得的最长公共子序列的长度。若不存在公共子序列,则输出仅有一行输出一个整数0。
样例输入
ABCBDAB
BDCABA
样例输出
4
解题思路
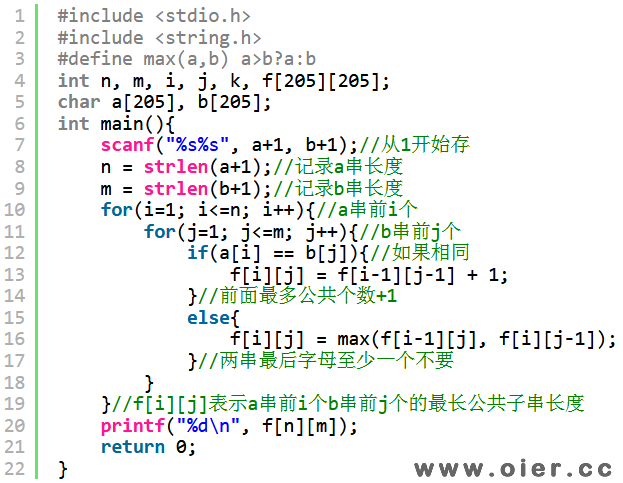
如果f[i][j]表示a串前i个字符b串前j个字符的最长公共子序列,那么f[i][j]可以通过前面的结果算出来。如果a[i]=b[j],那么最后这一对肯定要,因为要了之后只会更长不会更短,除去这一对字符,两个子串的最长公共子序列就是f[i-1][j-1];如果a[i]!=b[j],那么最后两个字符匹配不了,最长公共子序列一定不含a[i]或者不含b[j],f[i][j]要么取f[i-1][j](不要a[i])的值,要么取f[i][j-1](不要b[j])的值。只要我们从小到大依次计算,即先算f11、f12、f13……f21、f22、f23……那么算f[i][j]的时候,f[i-1][j-1]、f[i-1][j]以及f[i][j-1]都是已知的。
程序实现