题目大意:在n*n的棋盘上放置n个皇后,要求他们彼此不受攻击,请输出所有可行摆放方法。
题目描述
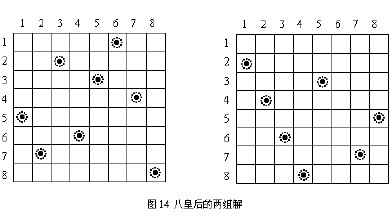
在n*n的棋盘上放置n个皇后(n<=10)而彼此不受攻击(即在棋盘的任一行,任一列和任一对角线上不能放置2个皇后),编程求解所有的摆放方法。
输入
输入: n
输出
每一行输出一种方案,每种方案顺序输出皇后所在的列号,每个数占五个字符的位。若无方案,则输出 “no solute.”。
样例输入
4
样例输出
2 4 1 3
3 1 4 2
解题思路
一个一个格子尝试放皇后,放的时候,看一下有没有冲突,没有就放下去,如果能放下n个皇后则输出。在写这个程序的时候,会发现,只要某一行放了一个皇后后,这一行其他格子都不用放了,也就是说,只需要确定每一行的皇后放在哪一列就行,只要就转换成了n个格子(n行)填数(放哪一列)的问题了。
一行一行递归搜索,这一行可以选择1到n列,只要没放过就可以放。一行只放一个,故行肯定没放过,不需要判断;列需要用一个数组记录,左右两斜也一样用数组记录。列很好办,斜的话需要找规律:左斜(左下角到右上角)的话同一斜行号和列号加起来是一样的,且各斜数字和不同;右斜(左上角到右下角)的话同一斜列号减行号的差是一样的,且各斜的差互不相同。为了防止右斜出现负数下标,给各斜的差加上一个比较大的数,数组稍微开大一点就行。
程序实现
代码中,x[i]记录第i行的皇后放在哪一列,y[i]记录第i列是否有皇后,z[i](i<21)记录左斜是否有皇后,z[i](i>25)记录右斜是否有皇后。
