SSOJ2348火车站（NOIP1998）
3064+
作者：crxis 发布：2017-08-12 分类：递推
题目大意：火车开出时车上有x人，第二个站上车y人、下车y人，之后上下车规律是上车人数是前两站上车之和，下车人数是上一站上车人数，到达低n站时有m人，那么第k站开出时有多少人？
题目描述
火车从始发站(称为第1站)开出，在始发站上车的人数为a，然后到达第2站，在第2站有人上、下车，但上、下车的人数相同，因此在第2站开出时（即在到达第3站之前）车上的人数保持为a人。从第3站起（包括第3站）上、下车的人数有一定的规律：上车的人数都是前两站上车人数之和，而下车人数等于上一站上车人数，一直到终点站的前一站（第n-1站），都满足此规律。现给出的条件是：共有n(n<20)个车站，始发站上车的人数为a，最后一站下车的人数是m（全部下车）。试问从x站开出时车上的人数是多少？
输入：a，n，m和x
输出：x站开出时车上的人数
样例：
输入：5 7 32 4
输出：13
输入
输入：a，n，m和x
输出
输出：x站开出时车上的人数
样例输入
5 7 32 4
样例输出
13
解题思路
设始发站有x人，到达第n站时有m人（第n-1站开出时有m人），不妨设第2站上下车都是y人，那么写一下找规律：
| 车站 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人数 | x | x | 2x | 2x+y | 3x+2y | 4x+4y | 4x+4y |
| 上车 | x | y | x+y | x+2y | 2x+3y | 3x+5y | 5x+8y |
| 下车 | 0 | y | y | x+y | x+2y | 2x+3y | 3x+5y |
| 差 | x | 0 | x | y | x+y | x+2y | 2x+3y |
| x | 1 | 0 | 1 | 0 | 1 | 1 | 2 |
| y | 0 | 0 | 0 | 1 | 1 | 2 | 3 |
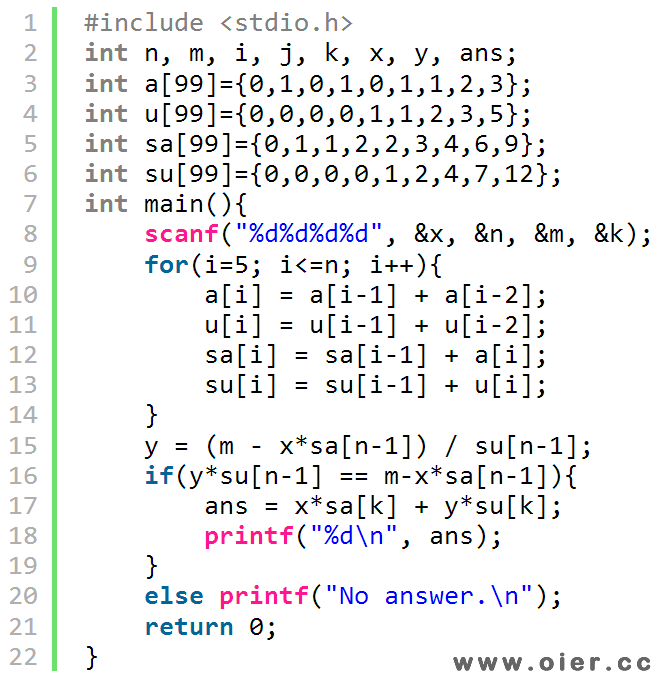
不难发现，之和上下车人数的差等于前两个站那个站上车的人数，其中x的常数和y的常数都是一个斐波拉契数列。只有我们求出这两个常数数组，并计算他们的前缀和，即可知道第k个站开出时的人数。第n-1个站开出时，人数是m，x、以及xy的常数都知道可以求出未知数y，最后代入求解第k个站的人数即可。
程序实现
