SSOJ2313最少转弯问题
6136+
作者:crxis 发布:2017-08-19 分类:广度优先搜索
题目大意:给你一张地图,告诉你哪些地方可以走,哪些地方不能走,问从起点到终点,至少转多少次弯?
题目描述
给出一张地图,这张地图被分为n*m(n,m<=100)个方块,任何一个方块不是平地就是高山。平地可以通过,高山则不能。现在你处在地图的(x1,y1)这块平地,问你至少需要拐几个弯才能达到目的地(x2,y2)?你只能沿着水平和垂直方向的地平上行进,拐弯次数就等于行进方向的改变(从水平到垂直或从垂直到水平)的次数。如图所示,最少的拐弯次数为5.
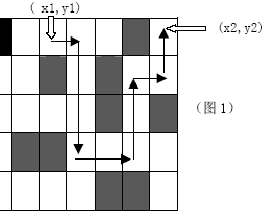
输入
第1行: n m
第2至n+1行:整个地图地形描述(0:空地;1:高山)
第2行地形描述为:1 0 0 0 0 1 0
第3行地形描述为:0 0 1 0 1 0 0
……
第n+2行:x1 y1 x2 y2(分别为起点、终点坐标)
输出
s(即最少的拐弯次数)
样例输入
5 7
1 0 0 0 0 1 0
0 0 1 0 1 0 0
0 0 0 0 1 0 1
0 1 1 0 0 0 0
0 0 0 0 1 1 0
1 3 1 7
样例输出
5
解题思路
跟迷宫填步数差不多,只是每次可能不止填4个格子,甚至需要填99*2个格子,因为同一条直路,转弯次数相同,即队列出来一个点,对于同一个方向的那些“下一步”的点,转弯次数都是出队点的转弯次数加1。虽然一次可能填很多个格子,但填过的不会重复再填,即入队不超过100*100,时间复杂度n的3次方。
程序实现
