SSOJ2299士兵站队问题
4317+
作者：crxis 发布：2017-07-05 分类：排序
题目大意：在一个网格操场上，士兵分散站着，现在要排除紧密的一行，士兵们至少总共走多少步？
题目描述
在一个划分成网格的操场上，n个士兵散乱地站在网格点上。网格点由整数坐标(x,y)表示。士兵们可以沿网格边上、下、左、右移动一步，但在同一时刻任一网格点上只能有一名士兵。按照军官的命令，士兵们要整齐地列成一个水平队列，即排列成(x,y),(x+1,y),…,(x+n-1,y)。如何选择x 和y的值才能使士兵们以最少的总移动步数排成一列。
编程任务：计算使所有士兵排成一行需要的最少移动步数。
输入
输入士兵数n，1<=n<=10000。接下来n 行是士兵的初始位置，每行2 个整数x 和y，-10000<=x，y<=10000。
输出
输出的第1 行中的数是士兵排成一行需要的最少移动步数。
样例输入
5
1 2
2 2
1 3
3 -2
3 3
样例输出
8
解题思路
1、确定纵坐标b的值：所有士兵都走到y=b这一行，那么b是所有y坐标中的中位数，代价为|y[1]-m|+|y[2]-m|+…+|y[n]-m|。对于这一行的纵坐标，如果往上偏移，那么“线上”的士兵都少走一步，“线下”的士兵都多走一步。只要线两边的士兵不平衡，只需要慢慢的让这条线往士兵多的一边偏移，步数就会减少。只有线两边士兵数量相同，步数最少。（奇数、偶数一样）
2、横坐标区域，可以枚举区域左端点l，然后最左边的士兵移到l，第二左边的士兵移到l+1……每个士兵移动的步数加起来就是代价（不超时）。
3、横坐标代价计算优化：x[1]-l + x[2]-(l+1) + … + x[n]-(l+n-1) 即x[1]-0-l + x[2]-1-l + … + x[n]-(n-1)-l，如果把横坐标x[i]全部转换成x[i]-(i-1)，那么问题就相当于所有士兵移动到新的横坐标的中位数的问题了。
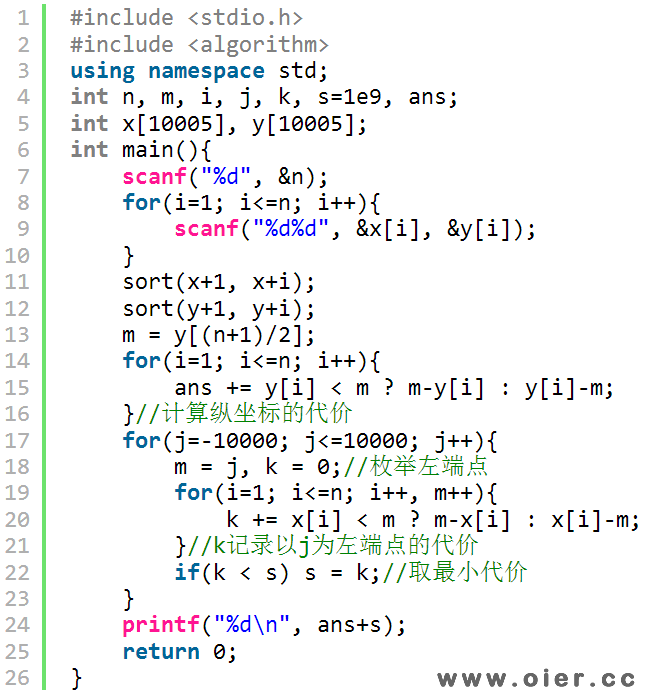
程序实现
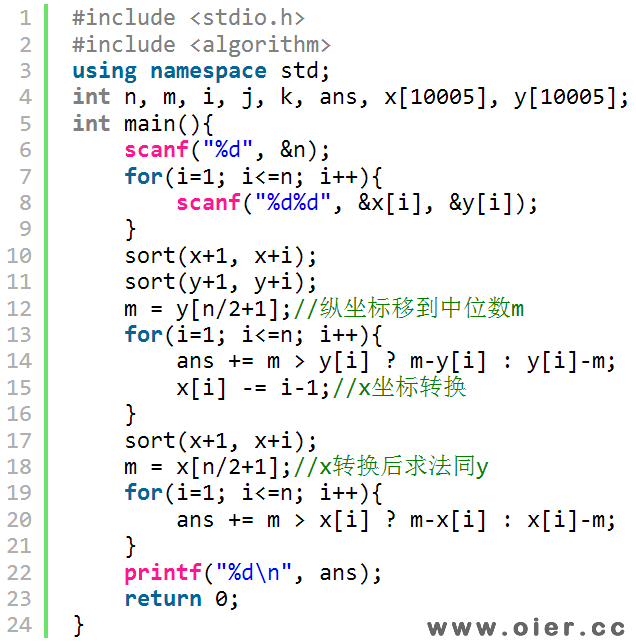
暴力拿分代码：
