题目大意:n个牧场有n-1条双向道路,现在需要在两个牧场之间的道路种草,请在种草前后回答某条道路有多少棵草?
题目描述
农夫约翰有N块贫瘠的牧场(2 <= N <= 100,000),有N-1条双向道路将这N个牧场连接了起来,每两个牧场间都有且仅有一条路径可相互到达。著名奶牛贝西经常抱怨:为什么连接牧场的道路上没有草可吃呢?
约翰非常喜欢贝西,今天约翰终于决定要在道路上种草了。约翰的种草工作被分成了M(1 <= M <=100,000)步操作。
在每一步中,下列两个事件中的一个会发生:
1.约翰会选择两个牧场,沿着两个牧场间的路径,在路径上的每一条道路上都种植1株牧草;
2.贝西会向约翰提问:在一条指定的道路上,种植了多少株牧草。
请帮助约翰回答贝西的问题。
输入
第一行有两个正整数N和M。
接下来N-1行,每行两个数,表示一条路径两端的牧场编号。
接下来M行,每行开头有一个字母,表示约翰的操作,P表示种植牧草,Q表示询问。接下来有两个数字,表示两个牧场的编号。
输出
对于每个询问,输出一行,一个数,表示该询问的答案。
样例输入
4 6
1 4
2 4
3 4
P 2 3
P 1 3
Q 3 4
P 1 4
Q 2 4
Q 1 4
样例输出
2
1
2
提示
《高级数据结构》例题12-2
来源:美国计算机竞赛 USACO 2011 Dec
解题思路
首先这是一棵树,确定根结点后,两个牧场之间的路径,就是他们分别到最近公共祖先的路径。现在需要统计每条道路(边)有多少棵草,我们可以用结点来记录,如果结点b的父亲是结点a,那么c[a]就表示a到b道路上的草的数量。暴力模拟,一步一步往上爬到公共祖先,如果遇到很大长链的话就会超时。因此,我们考虑用数量剖分的做法。
树链剖分,将一棵树划分成很多条链:从一个根结点开始,如果有儿子,就选择一个最重的儿子(子树结点数量最多)作为重儿子,重儿子也继续找重儿子,这样根结点与其所有重儿子的连边就是一条重链;对于其他非重儿子,分别看成“根结点”,也可以找到以自己为开头的重链。一步一步爬比较慢,我们就一条一条链往上爬!虽然有些重链结点数量比较少,甚至只有1个结点,但是,每次往上爬,爬到重链头的父亲后,其子树结点至少是原来子树结点数的2倍!也就是说至多爬log2n次。
为什么爬到另外一条重链后结点数会翻倍?
因为爬到另外一条重链,说明当前重链链头a只是新重链上某节点q的轻儿子,因为q的重儿子b所在子树的结点数量不比a少,所有结点数量至少翻倍。
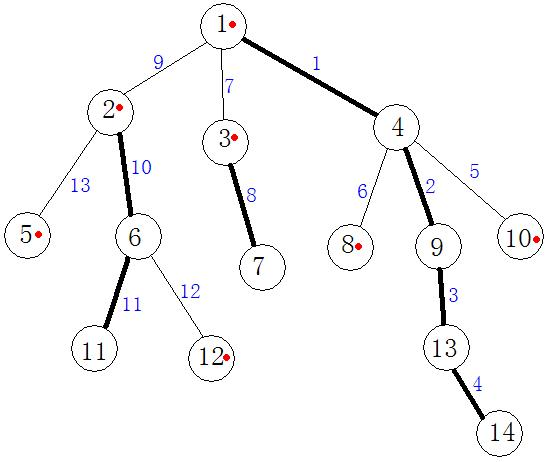
如上图,有红点的是重链链头,粗线是重边,边的编号是搜索顺序,结点重新编号后4是编号是2、3的编号是8……
将一棵树分成很多条链后, 需要实现区间加、区间求和,我们可以用线段树来维护。根据树的dfs序(有重儿子先搜索重儿子)对树的结点重新编号,那么一条重链就是连续的一段。如果要对一条链上的a到b的路径进行区间加,a和b的新编号分别是x和y,那么我们只需要对区间[x,y]进行加就行。接下来就想一下怎么爬!
如果在同一条重链上,只有一个区间,不需要爬;如果不在一条重链上,比较链头的深度,深度小的需要往上爬(深度大往上爬可能会涉及最短路径外的道路)。如结点a的新编号是id[a],那么从a爬到a的链头fa,需要处理的区间就是id[fa]到id[a],因为dfs搜索时,深度小的先搜索。对于最后一段路,因为点表示点往上的边,因此不涉及深度小的那个点往上那条边,区间左端点需要+1。
树链剖分各个数组的含义:fu数组记录结点父亲,从重链链头跳到另外一条重链时需要用到;zi数组记录重儿子,重新编号时需要先搜索重儿子;ge数组记录子树有多少个结点,用于找重儿子、子树区间修改等;v数组记录节点深度,用于比较链头深度确定谁先往上爬;top数组记录链头;id数组记录新的编号。
程序实现

以上是用线段树实现区间加1、单点求和:单点求和,不用用到非叶子结点的区间和,叶子结点的区间和就等于标记,故区间和的数组可以不开,直接用标记数组就行。
区间修改、单点查询,不难想到差分与树状数组。区间修改,我们可以在区间端点以及最近公共祖先位置打标记,求某个点的值时,只需要求子树的标记和即可。为了方便,结点编号倒着来,让子结点标号小,这样子树标记的区间就是根结点标号-子树结点数到根结点标号。
