题目大意：每天都需要用餐巾，可以购买，可以快洗、慢洗，价格各不同，什么时候买？什么时候快洗？什么时候慢洗？才能使费用最低？最低费用是多少？

题目描述

一个餐厅在相继的 N 天里，每天需用的餐巾数不尽相同。假设第 i 天需要 ri块餐巾(i=1，2，…，N)。餐厅可以购买新的餐巾，每块餐巾的费用为 p 分；或者把旧餐巾送到快洗部，洗一块需 m 天，其费用为 f 分；或者送到慢洗部，洗一块需 n 天(n>m)，其费用为 s

每天结束时，餐厅必须决定将多少块脏的餐巾送到快洗部，多少块餐巾送到慢洗部，以及多少块保存起来延期送洗。但是每天洗好的餐巾和购买的新餐巾数之和，要满足当天的需求量。

试设计一个算法为餐厅合理地安排好 N 天中餐巾使用计划，使总的花费最小。

编程找出一个最佳餐巾使用计划.

输入

第 1 行有 6 个正整数 N,p,m,f,n,s。N 是要安排餐巾使用计划的天数；p 是每块新餐巾的费用；m 是快洗部洗一块餐巾需用天数；f 是快洗部洗一块餐巾需要的费用；n 是慢洗部洗一块餐巾需用天数；s 是慢洗部洗一块餐巾需要的费用。接下来的 N 行是餐厅在相继的 N 天里，每天需用的餐巾数。

输出

将餐厅在相继的 N 天里使用餐巾的最小总花费输出

样例输入

3 10 2 3 3 2

5

6

7

样例输出

145

提示

n <= 1000

解题思路

此题是最小费用流，难在建图，建图后跑一遍最小费用流即可。

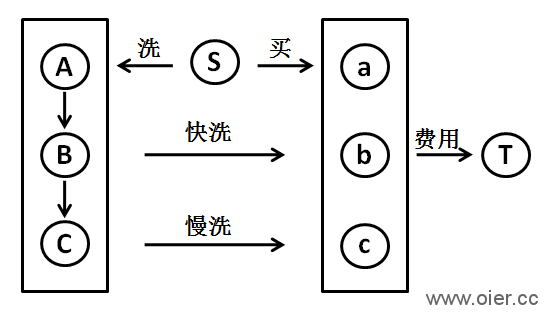
如图所示，小写字母表示每天需要用的餐巾，大写字母表示每天用完可以拿去洗的餐巾。

每天用的餐巾都是有费用，不管是购买还是洗，他的费用都需要累加起来，建图时汇于T点。（n条边）

这个餐巾可以购买（代码47行），可以通过快洗（代码51行）或者慢洗（代码50行）获得：购买价是p，可以购买无限条，但只需要解决当天就行，其他天需要的时候可以再买；快洗价是x，快洗后可以给洗完后任意时间使用；慢洗价是y，慢洗后可以给洗完后任意时间使用。（可以缩减到3*n条边）

为了能从S点出发，S向ABC集合建边（代码46行），当天最多出现r[i]块用过的餐巾。（n条边）

若洗完后，可以给之后任意一天使用，每天如此，则需要建立n的平方条边，容易超时。稍微优化一下，如A→B建立0费用无限流量边，让A天的餐巾可以留到下一天，即能用n条边取代n的平方条边。（代码49行）

图中每条边的费用是多少、流量是多少，请自己思考一下，想不出来可以稍稍看一下代码。

程序实现