题目大意:一个数列,一次放入Box,放入b[j]个后,回答第j小的是多少。
题目描述
Black Box是一种原始的数据库。它可以储存一个整数数组,还有一个特别的变量i。最开始的时候Black Box是空的.而i等于0。这个Black Box要处理一串命令。
命令只有两种:
ADD(x):把x元素放进BlackBox;
GET:i加1,然后输出Blackhox中第i小的数。
记住:第i小的数,就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如:
我们来演示一下一个有11个命令的命令串。(如下图所示)
| 编号 | 命令 | i | 黑匣子内容 | 输出 |
| 1 | ADD(3) | 0 | 3 | |
| 2 | GET | 1 | 3 | 3 |
| 3 | ADD(1) | 1 | 1,3 | |
| 4 | GET | 2 | 1,3 | 3 |
| 5 | ADD(-4) | 2 | -4,1,3 | |
| 6 | ADD(2) | 2 | -4,1,2,3 | |
| 7 | ADD(8) | 2 | -4,1,2,3,8 | |
| 8 | ADD(-1000) | 2 | -1000,-4,1,2,3,8 | |
| 9 | GET | 3 | -1000,-4,1,2,3,8 | 1 |
| 10 | GET | 4 | -1000,-4,1,2,3,8 | 2 |
| 11 | ADD(2) | 4 | -1000,-4,1,2,2,3,8 |
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串:1.A(1),A(2),…A(M):一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数,M$200000。例如上面的例子就是A=(3,1,一4,2,8,-1000,2)。
2.u(1),u(2),…u(N):表示第u(j)个元素被放进了Blaek Box里后就出现一个GET命令。例如上面的例子中u=(l,2,6,6)。输入数据不用判错。
输入
第一行,两个整数,M,N。
第二行,M个整数,表示A(l)……A(M)。
第三行,N个整数,表示u(l)…u(N)。
输出
样例输入
7 4
3 1 -4 2 8 -1000 2
1 2 6 6
样例输出
3
3
1
2
提示
对于30%的数据,M≤5000;
对于50%的数据,M≤10000;
对于70%的数据,M≤100000;
对于100%的数据,M≤200000。
解题思路
本题可以用堆、线段树、树状数组+离散化等实现。
程序实现
堆实现:两个优先队列,前一个大的在top,后一个小的在top;前面的堆先放入1个,保证里面刚刚好只有i个(一开始i=1,输出第i小);之和如果没有放完b[i]个数,就放入后面的堆,放的过程中,保存前一个是最小的i个,即如果发现放入的数字比前一个的top要小,则把前一个的top放入后一个,将新数放入前一个堆;放够b[i]个数后,输出前一个的top,因为那是最小的i个数中的最大值;那么下一次输出的是第i+1小,前一个堆不足i+1个,可以从后一个对中取最小的放过去,如果后一个对没有数,就从数列中放进去。

线段树做法:动态开点可以避免爆空间,因为只有n次单点修改。依次放入数列中的数,放够b[j]个就二分查找第k个数(区间),需要注意线段区间不能用int了!

树状数组:离散化后,可以用树状数组统计前i个数出现次数之和,二分树状数组寻找第k小的数。
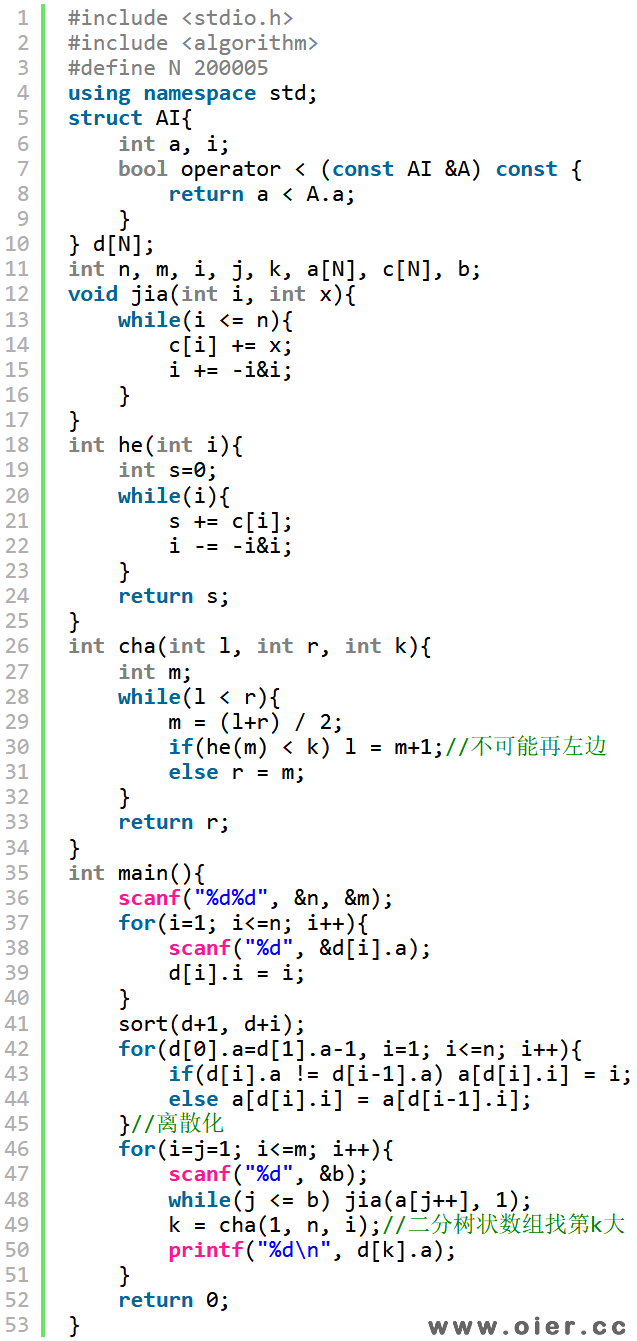
不会做到的话,可以暴力40分,每次回答对a数组前面b[j]个数进行排序,然后输出a[i],时间复杂度O(mnlog2n)。

暴力50分:快排查找第k小的数,复杂度是O(n)的,因为找到分界点后,第k小的数只会在其中一半,n+n/2+n/4+…+1不超过n*2。
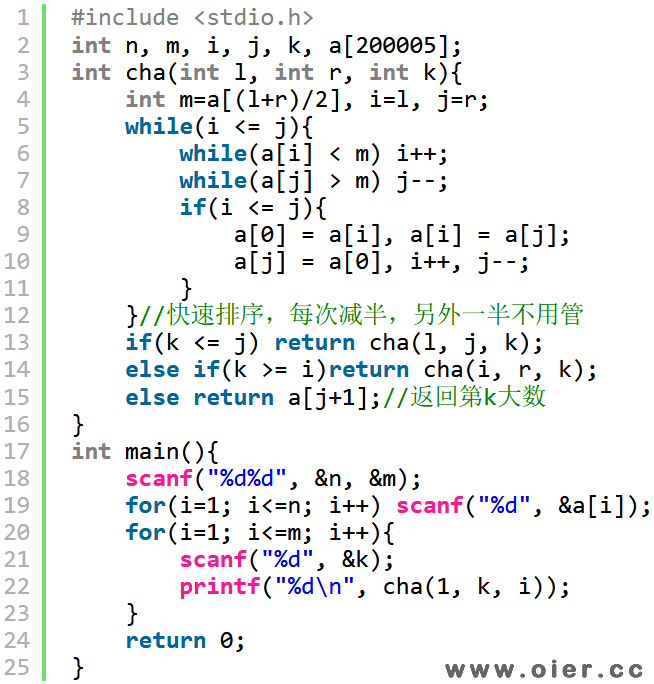
暴力50分:其实用插入排序就行,左边有序,插入排序的复杂度是O(n)的!
