题目大意:n个数,求编号是m的倍数的数的逆序对的总数。
题目描述
输入
第一行:输入一个正整数n和一个正整数m
接下来n行,每行一个整数。
输出
输出一个整数。
样例输入
5 2
-1
9
1
2
0
样例输出
5
提示
n以内m的倍数有2,4;
第2个数的逆序对有3个,分别是9和1,9和2,9和0
第4个数的逆序对有2个,分别是9和2, 2和0
这两个数的逆序对数量之和为3+2=5,所以输出5。
【数据范围】
30%的数据:m = 1,100%的数据:m < 10
数据1-10:n <= 5000,|ai|<=n,数据随机生成
数据11-12:n <= 10000,|ai|<=n,数据随机生成
数据13-14:n <= 50000,|ai|<=n,数据随机生成
数据15-16:n <= 100000,|ai|<=n,不重复,数据随机生成
数据17-18:n <= 100000,|ai|<2^31,不重复,数据随机生成
数据19-20:n <= 100000,|ai|<2^31,有重复,数据随机生成
解题思路
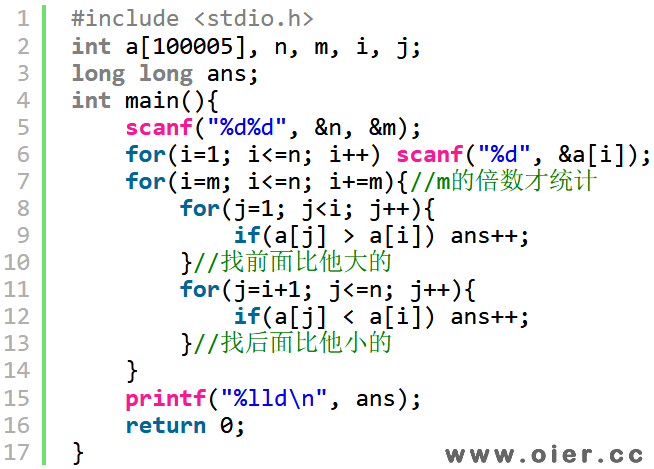
对于第i个数,他的逆序对数列是前面比他大的数的个数加上后面比他小的数的个数。暴力枚举一下:首先枚举m的倍数的编号,然后枚举前面和后面,统计逆序对之和,60分左右。
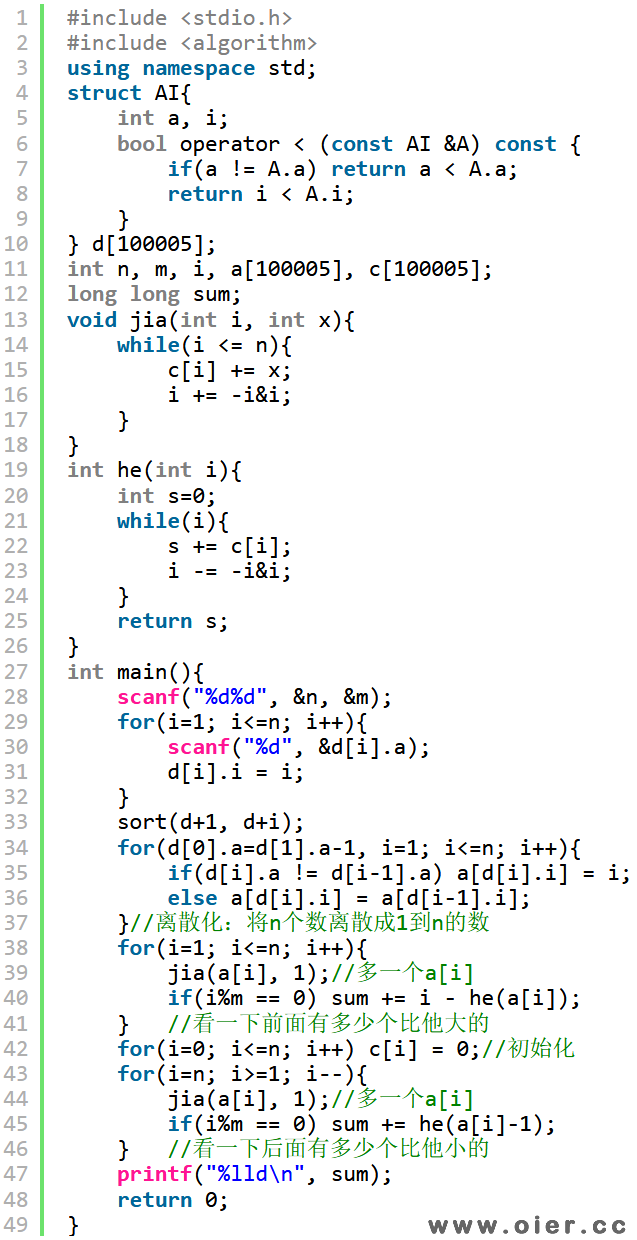
树状数组做法:从前往后一次加入a[i],加入后看一下树状数组中有多少个比他大的数,当前共有i个数,比他大的个数是i-he(a[i]);接下来找后面比他小的,那么需要从后往前加入树状数组,看当前共有多少个比他小的数,即he(a[i]-1)。这样只有80分,因为20%的数据是int范围,树状数组开不了那么大。要拿满分,可以先离散化,将这n个数映射到1到n中,就可以开一个大小为n的树状数组了。
线段树做法:思路跟树状数组差不多,只是不离散化也可以做,因为线段树支持动态开点。n次单点加1操作,每次至多用log2(2^32)个结点,空间开n*40就足够了。需要注意的是绝对值在int范围,避免负数需要加maxlongint,会超过int,因此区、编号间要用long long类型。
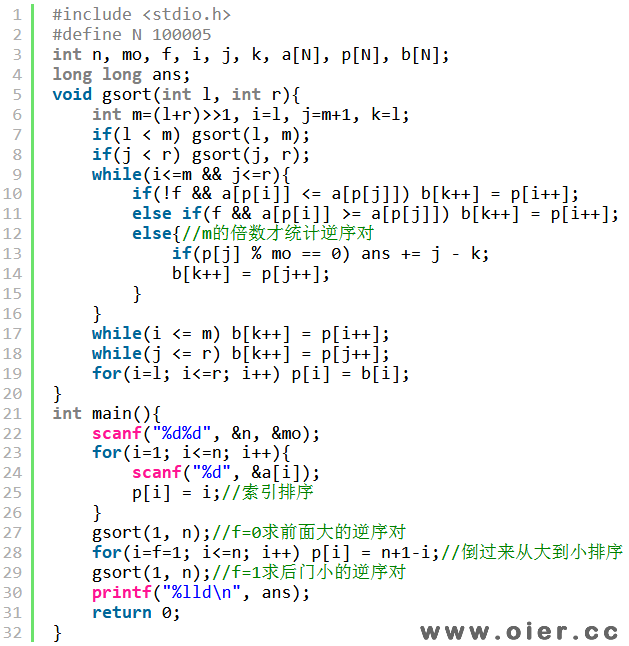
归并排序做法:在归并排序的时候,只统计编号是m的倍数的逆序对,不是m的倍数,就不加!可以开个结构体来排序,也可以直接用索引排序排编号。第一次求前面比他大的,需要从小到大排序;第二次求后面比他小的,需要把数组倒过来后从大到小排序。代码中p[i]记录的是原来数据的编号,因此看p[i]是不是m的倍数就可以确定是否需要加。
程序实现
树状数组
线段树

归并排序
暴力骗分: