题目大意:有m个魔法值为1到n的物品,按照一定的规则可以四个四个地组成魔法阵,第i个物品组成魔法阵的方案分别有哪些?
题目描述
六十年一次的魔法战争就要开始了,大魔法师准备从附近的魔法场中汲取魔法能量。
大魔法师有m个魔法物品,编号分别为1,2,…,m。每个物品具有一个魔法值,我们用Xi表示编号为i的物品的魔法值。每个魔法值Xi是不超过n的正整数,可能有多个物品的魔法值相同。
大魔法师认为,当且仅当四个编号为a,b,c,d的魔法物品满足xa<xb<xc<xd,Xb-Xa=2(Xd-Xc),并且xb-xa<(xc-xb)/3时,这四个魔法物品形成了一个魔法阵,他称这四个魔法物品分别为这个魔法阵的A物品,B物品,C物品,D物品。
现在,大魔法师想要知道,对于每个魔法物品,作为某个魔法阵的A物品出现的次数,作为B物品的次数,作为C物品的次数,和作为D物品的次数。
输入
输入文件的第一行包含两个空格隔开的正整数n和m。
接下来m行,每行一个正整数,第i+1行的正整数表示Xi,即编号为i的物品的魔法值。
输出
共输出m行,每行四个整数。第i行的四个整数依次表示编号为i的物品作 为A,B,C,D物品分别出现的次数。
保证标准输出中的每个数都不会超过10^9。
每行相邻的两个数之间用恰好一个空格隔开。
样例输入
输入样例#1:
30 8
1
24
7
28
5
29
26
24
输入样例#2:
15 15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
样例输出
输出样例#1:
4 0 0 0
0 0 1 0
0 2 0 0
0 0 1 1
1 3 0 0
0 0 0 2
0 0 2 2
0 0 1 0
输出样例#2:
5 0 0 0
4 0 0 0
3 5 0 0
2 4 0 0
1 3 0 0
0 2 0 0
0 1 0 0
0 0 0 0
0 0 0 0
0 0 1 0
0 0 2 1
0 0 3 2
0 0 4 3
0 0 5 4
0 0 0 5
限制
【子任务】
每个测试点的详细数据范围见下表。
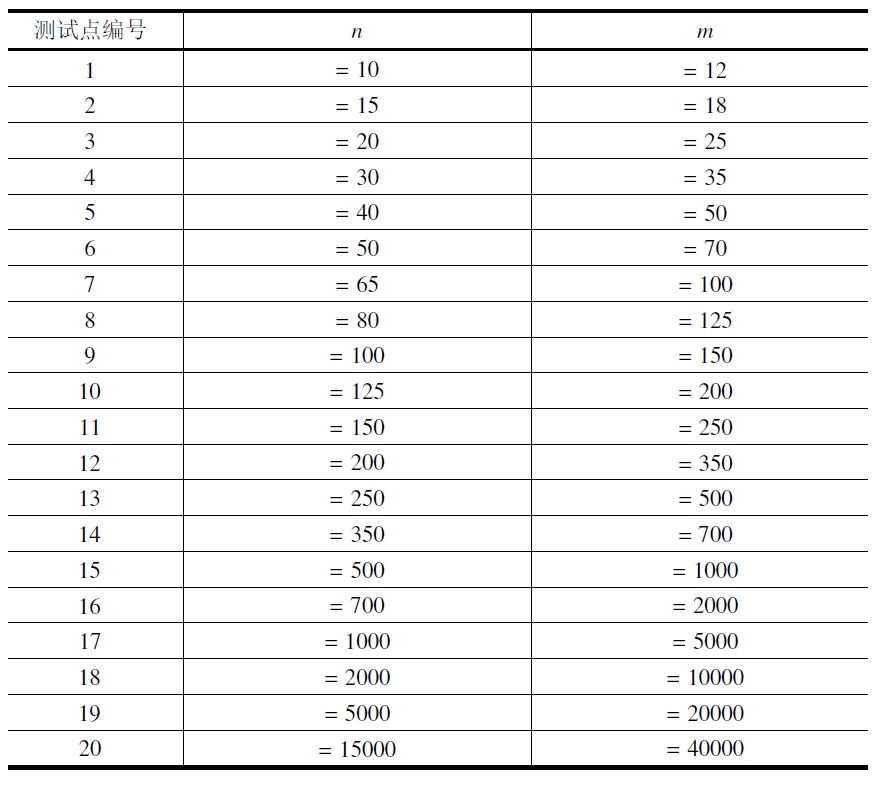
提示
【样例解释1】
共有5个魔法阵,分别为:
物品1,3,7,6,其魔法值分别为1,7,26,29;
物品1,5,2,7,其魔法值分别为1,5,24,26;
物品1,5,7,4,其魔法值分别为1,5,26,28;
物品1,5,8,7,其魔法值分别为1,5,24,26;
物品5,3,4,6,其魔法值分别为5,7,28,29。
以物品5为例,它作为A物品出现了1次,作为B物品出现了3次,没有作为C物品或者D物品出现,所以这一行输出的四个数依次为1,3,0,0。
此外,如果我们将输出看作一个m行4列的矩阵,那么每一列上的m个数之和都应等于魔法阵的总数。所以,如果你的输出不满足这个性质,那么这个输出一定不正确。你可以通过这个性质在一定程度上检查你的输出的正确性。
NOIP2016普及组第四题
解题思路
一开始会想到排序后枚举物品a、b、c、d,然后写起来觉得很烦,突然发现魔法阵相同的物品方案也相同,只需要枚举魔法值就行了。
枚举魔法值只需要枚举a、b、c,然后可以计算d,因为2*(d-c) = b-a,突然发现枚举d-c,再枚举a和c也是可以的,这样可以直接计算b和d,同样是枚举3个变量。
枚举过程中,不需要判断这个魔法值是否有物品,因为m比n大,数据随机分布,基本上覆盖所有魔法值,即使有0的,统计方案时也是加0,或者物品为0的魔法值方案数会增多而已。
在计算过程中,需要累加方案,还要考虑乘法原则,如abcd分别有2,1,1,1个,那么a作为1物品加1种方案,2作为2物品可以加2种方案,因为1物品有两种可选。
如何再缩减一重循环呢?在cd间隔相同的情况下,对于一对物品a和b,确定c和d后,后面更大的c和d也是符合要求的,所以我们可以倒着走:累加后面所有满足要求的c和d方案,即求后缀和。(ans[1][a] = f[b] * (f[c1]*f[d1] + f[c2]*f[d2] + … + f[ck]*f[dk]))这样的话,a和b的方案就可以快速统计出来,同理,求c和d的方案时,求对应a和b方案,后面乘其前缀和。
时间复杂度:O(n^2),因为外重循环是枚举到n/9,n*n/9不会超时。
程序实现

看不出前缀和、后缀和的话,还可以直接枚举间隔或者魔法值,也能拿到85分!


保证
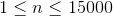
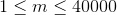
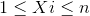 。
。
每个Xi是分别在合法范围内等概率随机生成的。