题目大意：在一个n*m的网格地上，有平原和山地，平原可以部署炮兵，炮兵攻击范围是长为5的十字型，请问最多能部署多少互不攻击的炮兵？

Description

司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成，地图的每一格可能是山地（用”H” 表示），也可能是平原（用”P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

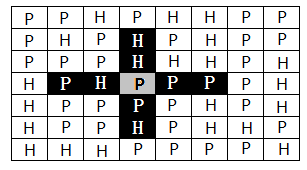
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

Input

Output

Sample Input

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

Sample Output

6

解题思路

状态中，1表示步数炮兵，0表示部署跑步，我们可以预处理每个状态有多少个炮兵，存储到y数组中。

行可行状态：首先，山地不能放炮兵，对于原来的地图，我们可以存储每一行的状态x，1表示对应位置有删掉，如果当前状态是y，且x&y不为0，那么山地放了炮兵，不可行；另外，炮兵攻击往左往右各两格，即两个炮兵至少隔两格，y&y<<1为0且y&y<<2也为0（包含了y&y>>1和y&y>>2的情况）。

状态转移：当前行的状态，不仅受上一行影响，还受再上一行的影响，因此状态需要涉及两行，f[i][j][k]表示第i行状态是j，i-1行状态是k的最多炮兵数，那么f[i][j][k]=f[i-1][k][l]+y[j]，即前一个状态的炮兵数加上当前行的炮兵数量，取最大值。

状态个数是1024，按照常规开数组会爆空间，我们可以考虑用滚动数组，或者用状态编号代替状态，因为可行编号不超过200（10个格子，隔两个放一个炮兵，最多能有多少种方案？）。

最后统计一下最后一行和倒数第二行的状态的炮兵数量，最后一行不放，就包含了前面的方案的最大数量了。

程序实现