题目大意:求两个整数序列的最长公共上升子序列,输出他的长度和编号字典序最小的序列。
题目描述
【题目描述】最长公共上升子序列(LCIS.cpp/c/pas)POJ 2127
研究发现,大猩猩的基因序列和人的基因序列只有1.3%的区别,更进一步,不仅仅离人最近的大猩猩和人的基因序列高度近似,就连以打洞为生的老鼠和人的基因序列也有高达95%的相同序列。于是有魔法师提出一个大胆设想,即改变人类的某些特定基因以期产生超级人类。
现在,他们要做的第一步是将两种不同生物的基因序列转换成两个整数序列,并试图确定他们的最大公共上升子序列的长度,例如有A序列为4 3 2 1 7 8 9,B序列为7 8 9 4 3 2 1,其最长公共子序列是4 3 2 1,而最长公共递增子序列应该是 7 8 9。
输入
输入每个序列由M个整数组成(1 ≤ M ≤500),M个整数范围在(-231 ≤Bi < 231)之间。
输出
第一行输出最长公共上升子序列长度L,第二行输出该子序列,如果该序列有多个答案,输出任意序列1的编号字典序最小的一个。
样例输入
5
1 4 2 5 -12
4
-12 1 2 4
样例输出
2
1 4
提示
输出按第一个序列的数字的编号字典需最小的那一组最长公共子序列
解题思路
按照最长上升子序列的思想,枚举序列的末尾以及前一个相同的位置,由前一个位置转移到后一个位置即可。由于有2个序列,故定义二维状态f[i][j]表示以a[i]和b[j]结尾的最长公共上升子序列的长度,前一个状态f[x][y]必须满足x<i&&y<j&&a[x]==b[y]&&a[x]<a[i],即满足“前一个”、“公共”、“上升”等条件。记录路径的话,我们只需要再开一个二维数组,记录i、j位置的前一个位置在哪就行,当然也可以用一维数组,把位置压成一个数,如i=1,j=1的位置记作1*501+1=501,递归输出时只需要整除或者取模即可获取序列1中的位置、序列2中的位置。
程序实现

时间优化
如果按照最长公共子序列,我们会想到定义f[i][j]表示序列1前i个数序列2前j个数的最长公共上升子序列,但这样就不知道以哪个数结尾,是无法确定上升序列的。为了解决上升问题,我们可以定义f[i][j]表示序列1以a[i]结尾、序列2中前j个数的最长公共上升子序列,这样里面就不需要枚举j前面的数了,因为如果k1>k2,那么f[i][k1] > f[i][k2],序列2并没有要求结尾,肯定越长越好。与最长公共子序列不同的是,如果两个数不相等,f[i][j]只能等于f[i][j-1],不能等于f[i-1][j],因为f[i-1][j]是以a[i-1]结尾的。
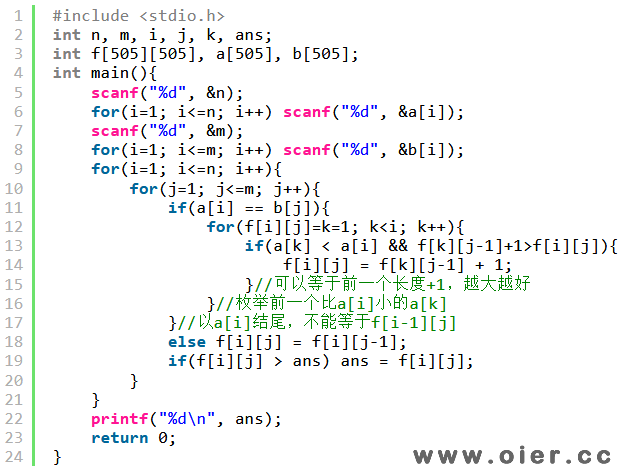
如果交换一下枚举i和枚举j的两重循环的顺序,也是可以计算出正确答案的,因为在计算f[i][j]时,f[k][j-1]和f[i][j-1]以及枚举过并计算出最优值。这是我们发现,i是从小到底枚举的,我们要求的以i前面的i-1个数结尾的最大值可以顺便求出来。在求完f[i][j]后,如果a[i]比b[j]要小(因为后面遇到相等,a[i]就是前一个数,要更小),那么f[i][j-1]可以直接跟以序列1中i前面的比b[j]要小的数结尾的序列的最大值f[k][j-1]进行比较,从而维护序列1前面最后一个数比b[j]小的最长公共子序列的最大长度。
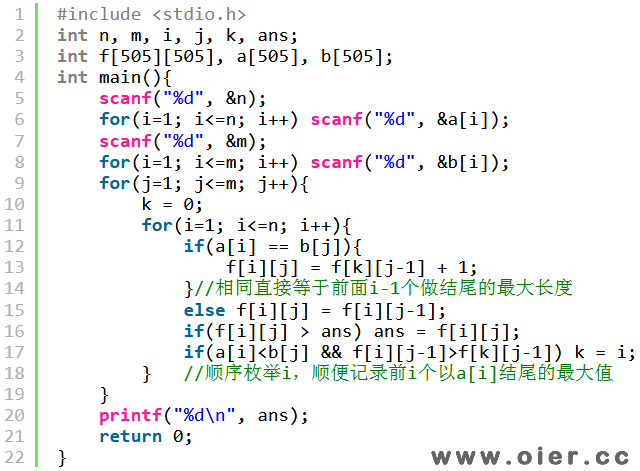
写出上述代码后,发现更小f[i][j]只用到f[i][j-1],可以降维压缩空间。为什么可以降到1维呢?第13行代码,f[k][j-1]其实就是f[k],因为这个时候f[k]还没更新;第15行可以直接不写,因为自己等于自己;17行中的f[i][j-1]可以写成f[i][j],因为a[i]<b[j]即a[i]!=b[j],f[i][j]就等于f[i][j-1],用的还是前一次的数据。需要注意的是,f[i]不能直接等于f[k]+1,因为f[i]里面是有数据的。
