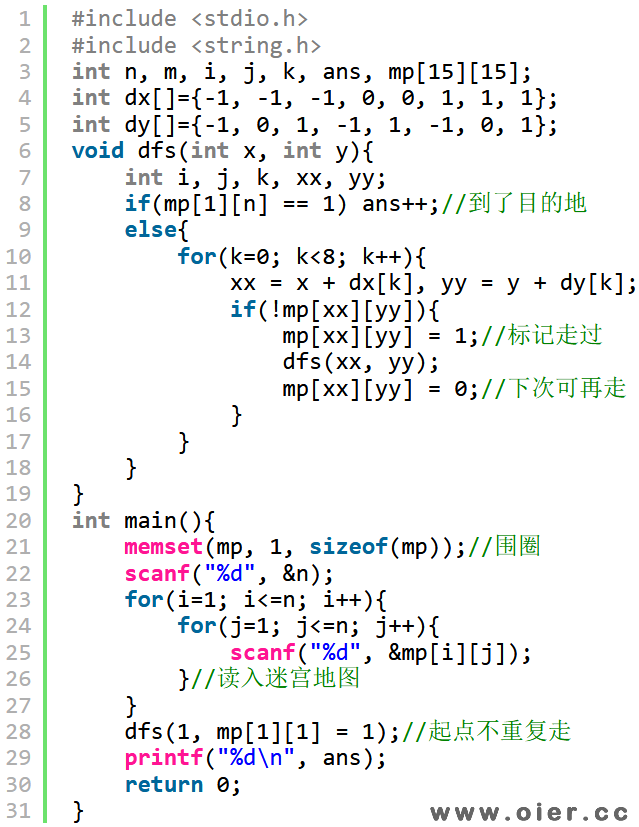
SSOJ1439迷宫问题
6198+
作者:crxis 发布:2018-05-22 分类:深度优先搜索
题目大意:一个n*n的迷宫,0可以到达1不可以到达,可以往8个方向走,从左上角走到右上角,共有多少走走法?
题目描述
设有一个N*N(2<=N<=10)方格的迷宫,入口和出口分别在左上角和右上角。迷宫格子中分别放0和1,0表示可通,1表示不能通过,入口和出口处肯定是0.迷宫走的规则如下所示:即从某点开始,有八个方向可走,前进方格中数字为0时表示可通过,为1时表示不可以通过,要另找路径。找出所有从入口(左上角)到出口(右上角)的路径(不能重复),输出路径总数,如果无法到达,则输出0.
输入
第一行方格迷宫的大小n
接着n行,每行n列,数字之间有空格
输出
输出路径总数
样例输入
3
0 0 0
0 1 1
1 0 0
样例输出
2
解题思路
从左上角出发,往8个方向走,走到下一个格子后,继续这样做,直到到达终点右上角,即找到一条路径。
找到路径后,退一步继续往其他方向走,试探其他路径。退回上一步后,继续往其他方向走,是不会重复走当前方向的,因为(代码第10行)k++后,方向变化了,所以每次找到的路径都是不同的。
注意,代码判断走到右上角的条件是右上角格子走过(mp[1][n]==1),这样的话,走到右上角后不能继续走,因为继续做,右上角一直是1,就会多加很多条路径。
程序实现