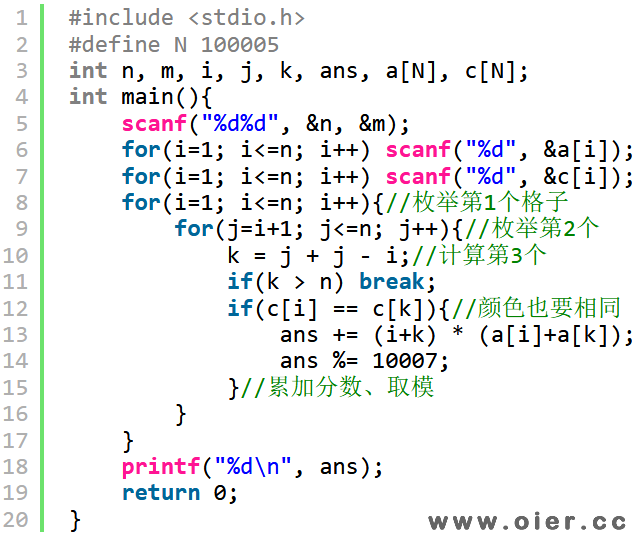
题目大意:n个格子,每个格子有编号、颜色和数字,当两个满足颜色相同、中间有格子,就能产生分数,请问总分模10007是多少?
题目描述
一条狭长的纸带被均匀划分出了 n 个格子,格子编号从 1 到 n。每个格子上都染了一种颜色colori(用[1,m]当中的一个整数表示),并且写了一个数字numberi。
定义一种特殊的三元组:(x, y, z),其中 x,y,z 都代表纸带上格子的编号,这里的三元组要求满足以下两个条件:
- x, y, z都是整数, x < y < z, y − x = z − y
- colorx = colorz
满足上述条件的三元组的分数规定为(x + z) ∗ (numberx + numberz)。整个纸带的分数规定为所有满足条件的三元组的分数的和。这个分数可能会很大,你只要输出整个纸带的分数除以 10,007 所得的余数即可。
输入
第一行是用一个空格隔开的两个正整数 n 和 m,n 代表纸带上格子的个数,m 代表纸带上 颜色的种类数。
第二行有 n 个用空格隔开的正整数,第 i 个数字numberi代表纸带上编号为 i 的格子上面写的数字。
第三行有 n 个用空格隔开的正整数,第 i 个数字colori代表纸带上编号为 i 的格子染的颜色。
输出
共一行,一个整数,表示所求的纸带分数除以 10,007 所得的余数。
样例输入
样例输入1
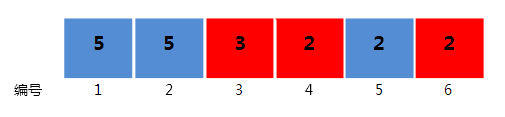
6 2
5 5 3 2 2 2
2 2 1 1 2 1
样例输入2
15 4
5 10 8 2 2 2 9 9 7 7 5 6 4 2 4
2 2 3 3 4 3 3 2 4 4 4 4 1 1 1
样例输出
样例输出1
82
样例输出2
1388
提示
对于第 1 组至第 2 组数据,1 ≤ n ≤ 100, 1 ≤ m ≤ 5; 对于第 3 组至第 4 组数据,1 ≤ n ≤ 3000, 1 ≤ m ≤ 100;
对于第 5 组至第 6 组数据,1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000,且不存在出现次数超过 20 的颜色;
对于全部 10 组数据, 1 ≤ n ≤ 100000, 1 ≤ m ≤ 100000, 1 ≤ colori ≤ m, 1 ≤ numberi ≤ 100000。
NOIP2015普及组第三题
解题思路
暴力枚举可得40分:枚举第一个格子编号x和第二个格子编号y,有y-x=z-y可得z=y+y-x。x的枚举范围是1到n,y的枚举范围是x+1到n,如果x和z颜色相同,那么累加分数。时间复杂度O(n*n)。
第5、6组数据,颜色不超过20,是在提示可以分开颜色来处理。结构体记录编号、颜色、数字,按照颜色排序后,每种颜色暴力求得分就可以通过了。为什么呢?每一种颜色暴力的代价是20*20,最多有100000种颜色(实际上是5000),总的计算次数在千万级别内,不超时。
既然可以分开颜色,当然也可以分开奇偶性。x和z中间有一个格子,那么x和z奇偶性必定相同。奇偶性相同、颜色也相同的格子,才能够产生分数。按颜色及奇偶性分类后,同颜色同奇偶性的格子,产生的分数,是有规律的——任意两个格子都可以产生分数,通过乘法分配了可O(1)算出一个格子编号成了多少次。如颜色为红色、编号为奇数的格子共有10个,那么第一个格子需要分别与另外9个格子产生分数,i1*i1+i1*i2 + i1*i1+i1*i3 + … + i1*i1+i1*i10 = i1*s + i1 * (10-2)。
得出公式后,我们不需要排序了,只需要统计每一种颜色为奇数和偶数的个数以及格子数字之和就行,时间复杂度O(n)。
程序实现
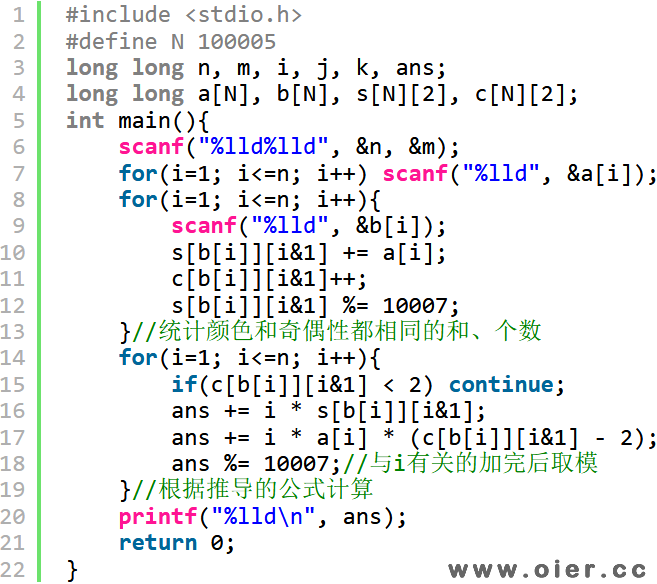
暴力40分: