题目大意:两盒火柴各有n根,火柴分别与另外一盒中的1根不重复地配对,如何配对才能使各对差的平方的和最小?原来已有配对,至少交换多少次才能得到最优配对?
题目描述
涵涵有两盒火柴,每盒装有 n 根火柴,每根火柴都有一个高度。现在将每盒中的火柴各自排成一列,同一列火柴的高度互不相同,两列火柴之间的距离定义为:∑(ai-bi)^2,其中 ai表示第一列火柴中第 i 个火柴的高度,bi表示第二列火柴中第 i 个火柴的高度。
每列火柴中相邻两根火柴的位置都可以交换,请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离,最少需要交换多少次?如果这个数字太大,请输出这个最小交换次数对 99,999,997 取模的结果。
输入
共三行,第一行包含一个整数 n,表示每盒中火柴的数目。
第二行有 n 个整数,每两个整数之间用一个空格隔开,表示第一列火柴的高度。
第三行有 n 个整数,每两个整数之间用一个空格隔开,表示第二列火柴的高度。
输出
输出共一行,包含一个整数,表示最少交换次数对 99,999,997 取模的结果。
样例输入
[Sample 1]
4
2 3 1 4
3 2 1 4
[Sample 2]
4
1 3 4 2
1 7 2 4
样例输出
[Sample 1]
1
[Sample 2]
2
提示
【样例1说明】最小距离是 0,最少需要交换 1 次,比如:交换第 1 列的前 2 根火柴或者交换第 2 列的前 2 根火柴。
【样例2说明】最小距离是 10,最少需要交换 2 次,比如:交换第 1 列的中间 2 根火柴的位置,再交换第 2 列中后 2 根火柴的位置。
【数据范围】
对于 10%的数据, 1 ≤ n ≤ 10;
对于 30%的数据,1 ≤ n ≤ 100;
对于 60%的数据,1 ≤ n ≤ 1,000;
对于 100%的数据,1 ≤ n ≤ 100,000,0 ≤火柴高度≤ 2^31 – 1。
NOIP2013提高组第一天第二题
解题思路
配对方案:两盒火柴的第i小分别配对,这样距离最小,这根方差、正方形长方形的面积很相似,你可以尝试举反例:对于两列火柴a、b和c、d,要么ac配对,要么ad配对,两种配对的距离差是2*(ad+bc-ac-bd) = 2*( a*(d-c) + b*(c-d) ),如果要ac配对,那么距离差要是负数,要让他是负数即a<b&&c<d或者a>b&&c>d,即大的跟大的配对,小的跟小的配对。对于任意两根相邻的火柴,通过此方法比较,就知道是否需要交换了。
两列火柴排好序后,可以得到一一对应的关系:如果第二列火柴不动,那么第一列火柴中原来位置为i火柴的要排到第二列火柴中跟他排名相同的火柴的原来位置j,令c[i]=j,对c数组排序后c[i]就会走到j的位置了(因为c数组的值是1到n),排序至少要交换多少次即最少交换次数,可以用归并排序来求(逆序对)。
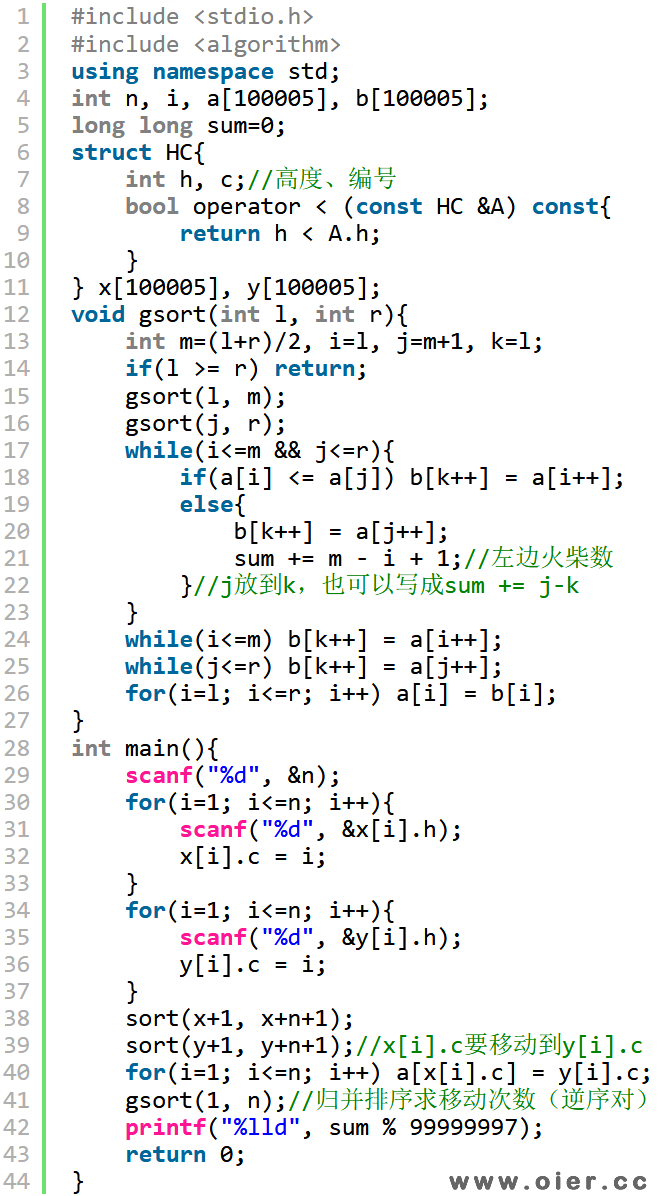
程序实现