题目大意:n个人围成一圈,分别在0到n-1位置,每次旋转m位(0到m、1到m+1的位置),10^k次旋转后,原来在x位置的会到哪个位置?
题目描述
n 个小伙伴(编号从 0 到 n-1)围坐一圈玩游戏。按照顺时针方向给 n 个位置编号,从0 到 n-1。最初,第 0 号小伙伴在第 0 号位置,第 1 号小伙伴在第 1 号位置,……,依此类推。
游戏规则如下:每一轮第 0 号位置上的小伙伴顺时针走到第 m 号位置,第 1 号位置小伙伴走到第 m+1 号位置,……,依此类推,第n – m号位置上的小伙伴走到第 0 号位置,第n-m+1 号位置上的小伙伴走到第 1 号位置,……,第 n-1 号位置上的小伙伴顺时针走到第m-1 号位置。
现在,一共进行了 10^k 轮,请问 x 号小伙伴最后走到了第几号位置。
输入
输入共 1 行,包含 4 个整数 n、m、k、x,每两个整数之间用一个空格隔开。
输出
输出共 1 行,包含 1 个整数,表示 10^k 轮后 x 号小伙伴所在的位置编号。
样例输入
10 3 4 5
样例输出
5
提示
对于 30%的数据,0 < k < 7;
对于 80%的数据,0 < k < 10^7;
对于 100%的数据,1 < n < 1,000,000,0 < m < n,1 <= x <=n,0 < k < 10^9。
NOIP2013提高组第一天第一题
解题思路
每进行一次游戏,x的位置都会增加m,如果超过n-1,那么取模就是他的新位置。因此,我们只需要计算x+m*10^k,就知道x的最终位置了。对于80%的数据,暴力计算10^k是可以通过的,甚至可以拿到90分!更快的方法是使用快速幂,如求10^5,可以看成是10^4*10^1,对于每一个10^k,都可以转成不超过30个的10^(2^i)的因子,即如果k的二进制表示中,如果个位有1,则需要乘以10^1,如果“千位”有1,则需要乘以10^8,而10^1、10^2、10^4、10^8、10^16、10^32……可以依次递推出来。
程序实现
将k转成二进制的过程中,判断末位二进制是否1,是的话乘以对应的倍数,倍数每次需要平方。
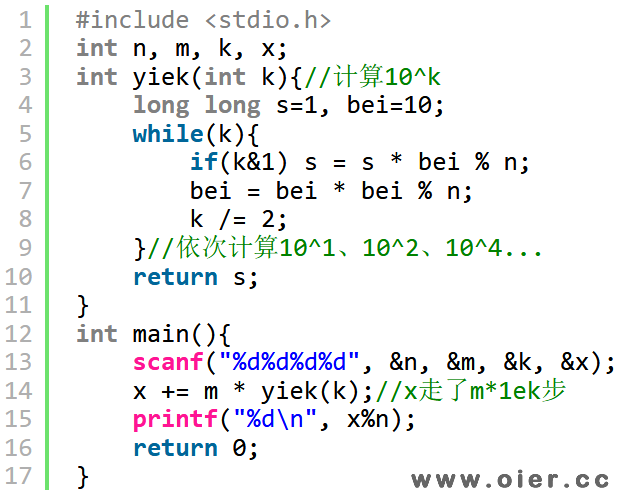
O(1)算法,直接枚举30位,如果k的二进制中有该位1,乘以对应的倍数。

暴力计算10^k,好像可以获得90分!
