题目大意:n个物品,有价格和重要度,每个物品的价值为价格*重要度,花费不超过m,最大价值是多少?
题目描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过N 元钱就行”。今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的N 元。于是,他把每件物品规定了一个重要度,分为5 等:用整数1~5 表示,第5 等最重要。他还从因特网上查到了每件物品的价格(都是整数元)。他希望在不超过N 元(可以等于N 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第j 件物品的价格为v[j],重要度为w[j],共选中了k 件物品,编号依次为j1…jk,则所求的总和为:v[j1]*w[j1]+..+v[jk]*w[jk]
请你帮助金明设计一个满足要求的购物单.
输入
输入的第1 行,为两个正整数,用一个空格隔开:
N m (其中N(< 30000)表示总钱数,m(< 25)为希望购买物品的个数。)
从第2 行到第m+1 行,第j 行给出了编号为j1 的物品的基本数据,每行有2 个非负整数
v p (其中v 表示该物品的价格(v≤10000),p 表示该物品的重要度(1~5))
输出
输出只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的 最大值(< 100000000)
样例输入
1000 5
800 2
400 5
300 5
400 3
200 2
样例输出
3900
提示
NOIP2006普及组第二题
解题思路
这是一道01背包的模板题,DP做法暂时不讲,下面我没看搜索的做法。
每个物品要么选,要么不选,n个格子填0和1,暴力枚举完选不选后,统计花费和价值,记录不超过m的花费的最大价值即可。
如果最后在统计,时间复杂度是O(2^n * n),虽然25很小,但也必定超时,所以必须剪枝。
首先,我们可以把计算过程记录下来,避免最后再统计花费、价值,时间复杂度降到O(2^n),当然如果n=25还是会超时。
其次,我们需要利用中间过程的值进行剪枝,如花费已经超过m,后面就没必要搜下去了。
最后,我们还可以进行记忆化,记录搜到第k个物品(剩下k到n个物品没选),价值为x的最大价值,如果下次再遇到同样情况或者更差情况——同样花费价值更小,那就剪枝,因为后面剩下的物品一样,选法一样,最大价值也一样。
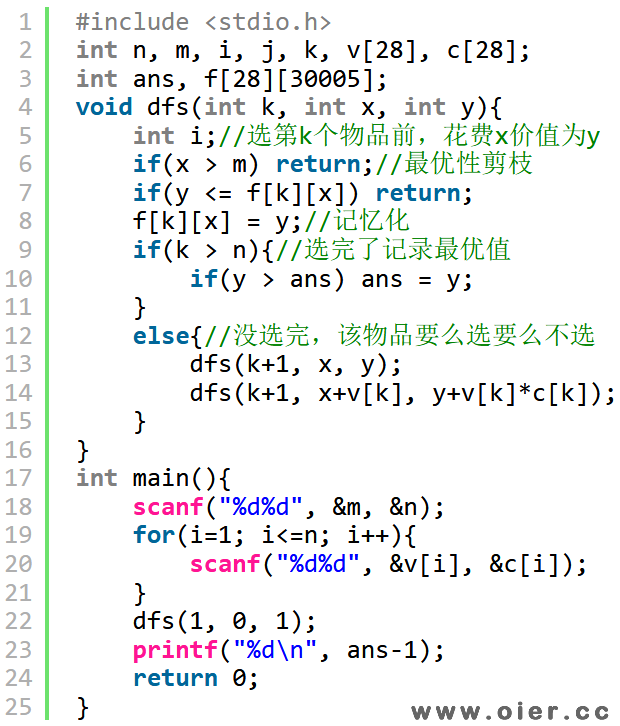
程序实现