SSOJ1257合唱队形（NOIP2004）
3387+
作者：crxis 发布：2017-10-26 分类：序列DP
题目大意：n个同学排合成队形，要求从左到右到左是越来越高在越来越矮，不改变原来顺序，至少要请多少位同学出列？
题目描述
N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K位同学排成合唱队形。
合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1，2…，K，他们的身高分别为T1，T2，…，TK， 则他们的身高满足
T1< …< Ti> Ti+1> …> TK(1< =i< =K)。
你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。
输入
输入的第一行是一个整数N(2< =N< =100)，表示同学的总数。第一行有n个整数，用空格分隔，第i个整数Ti(130< =Ti< =230)是第i位同学的身高(厘米)。
输出
输出包括一行，这一行只包含一个整数，就是最少需要几位同学出列。
样例输入
8
186 186 150 200 160 130 197 220
样例输出
4
提示
NOIP2004提高组第三题
解题思路
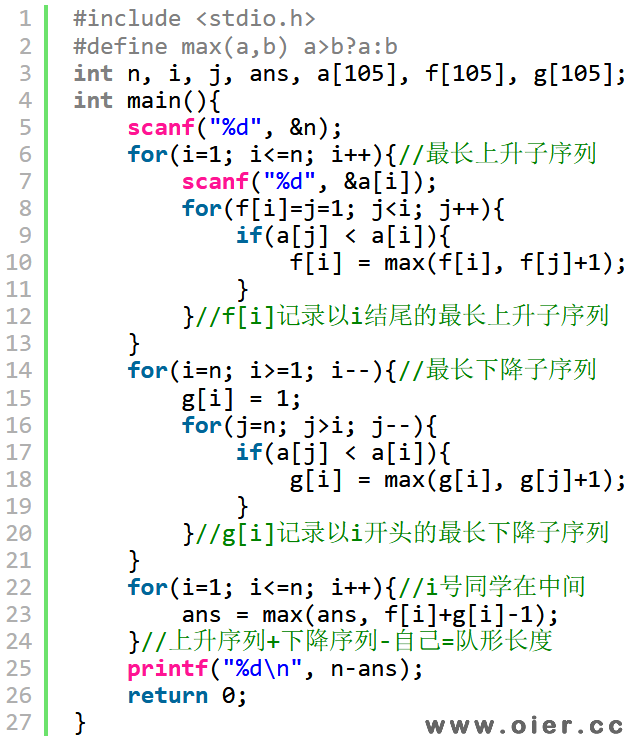
左边是一个上升序列，右边是一个下降序列，只要确定中间那个同学，左边越长越好，右边也越长越好。我们可以预处理出每位同学左边最多能站多少人（最长上升子序列），右边最多能占多少人（最长下降子序列），最后枚举每个同学做最高点计算队形长度，出列人数即n-队形人数。程序中f[i]表示以第i个同学为最高点，最长上升子序列是多少，g[i]表示以第i个同学为最高点，最长下降子序列是多少。
程序实现
