题目大意:有m种饲料,n种维生素,如何选最少种类的饲料,使得选择的饲料含有n种维生素且各种维生素不低于限制?
题目描述
纪念“逝去”的余世剑(cao shuo啊)
农民JOHN以拥有世界上最健康的奶牛为傲。他知道每种饲料中所包含的牛所需的最低的维他命量是多少。请你帮助农夫喂养他的牛,以保持它们的健康,使喂给牛的饲料的种数最少。
给出牛所需的最低的维他命量,输出喂给牛需要哪些种类的饲料,且所需的饲料剂量最少。
维他命量以整数表示,每种饲料最多只能对牛使用一次,数据保证存在解。
输入
第1行:一个整数V(1<=V<=25),表示需要的维他命的种类数。
第2行:V个整数(1<=每个数<=1000),表示牛每天需要的每种维他命的最小量。
第3行:一个整数G(1<=G<=15),表示可用来喂牛的饲料的种数。
下面G行,第n行表示编号为n饲料包含的各种维他命的量的多少。
输出
输出文件只有一行,包括
牛必需的最小的饲料种数P
后面有P个数,表示所选择的饲料编号(按从小到大排列)。
如果有多个解,输出饲料序号最小的(即字典序最小)。
样例输入
4
100 200 300 400
3
50 50 50 50
200 300 200 300
900 150 389 399
样例输出
2 1 3
解题思路
暴力枚举每一种饲料选不选,即填0和1,填完后验证是否满足条件——统计各种维生素的量,若都达到基本需求,则可行,记录最小值及方案。
程序实现
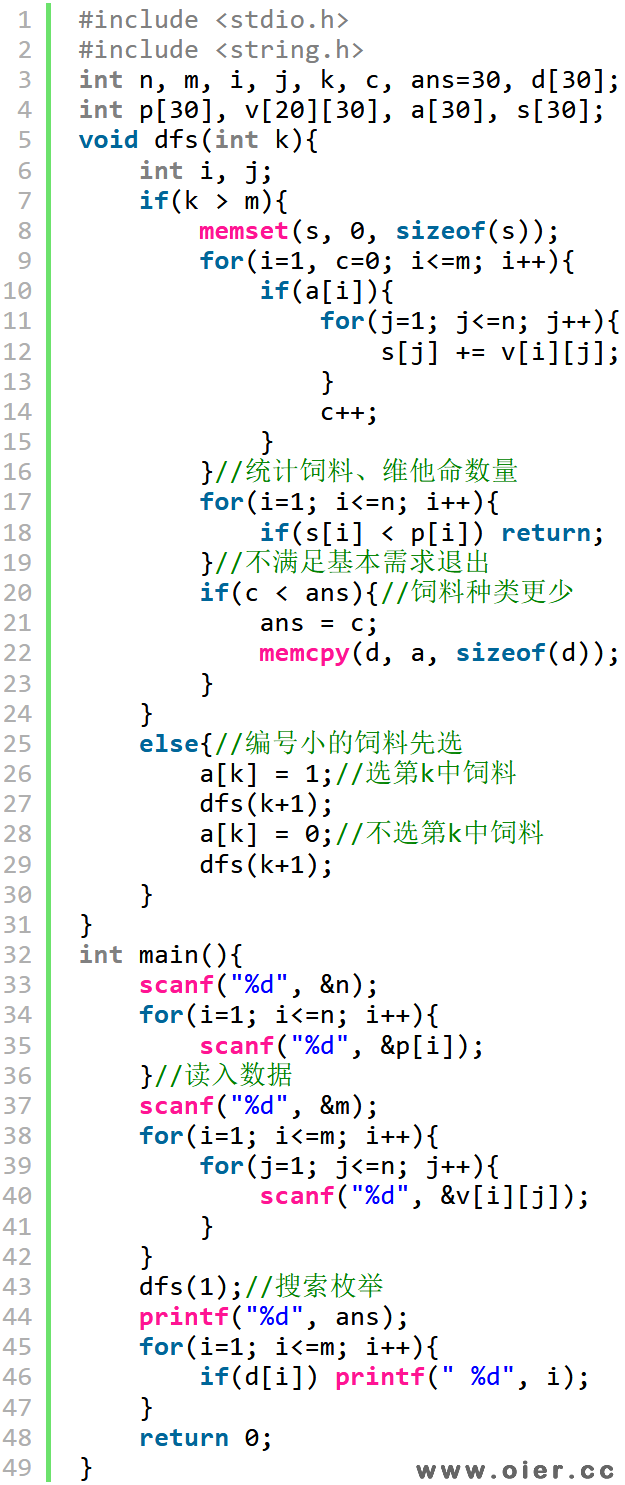
暴力搜索,时间复杂度O(2^n * m*n)。
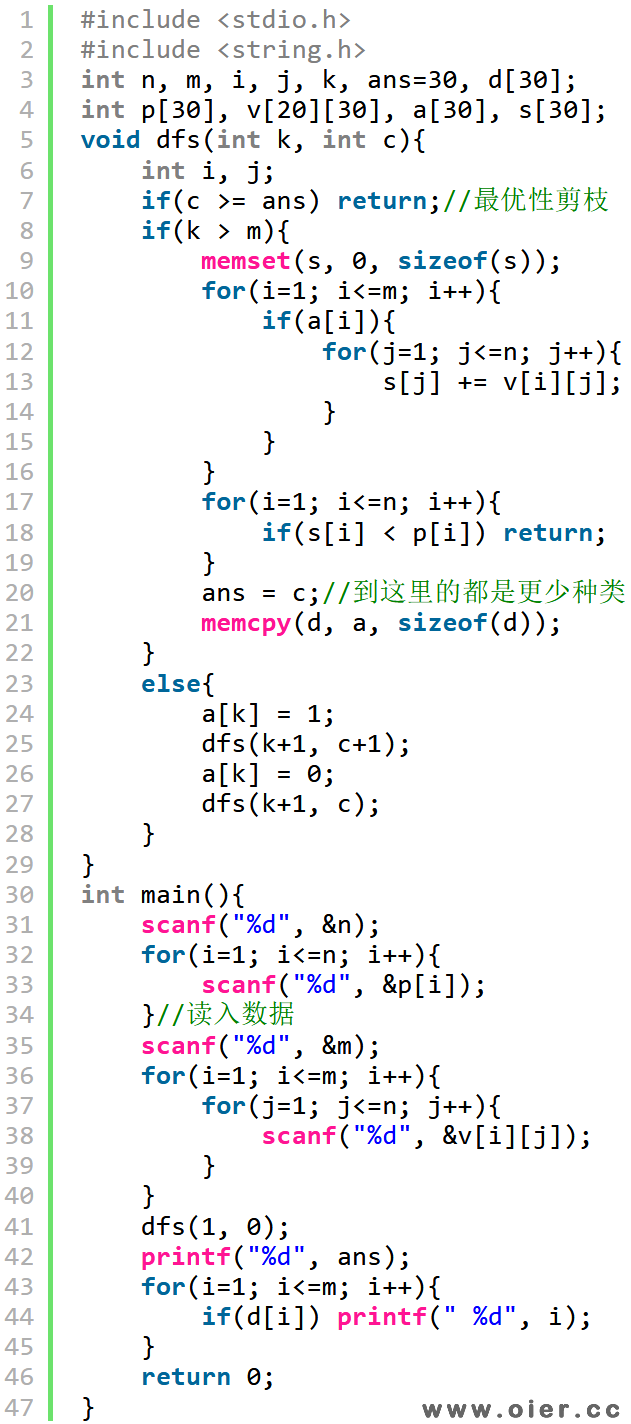
加了个最优性剪枝,如果当前选择的饲料种数超过最优值,后面不需要再看下去了。
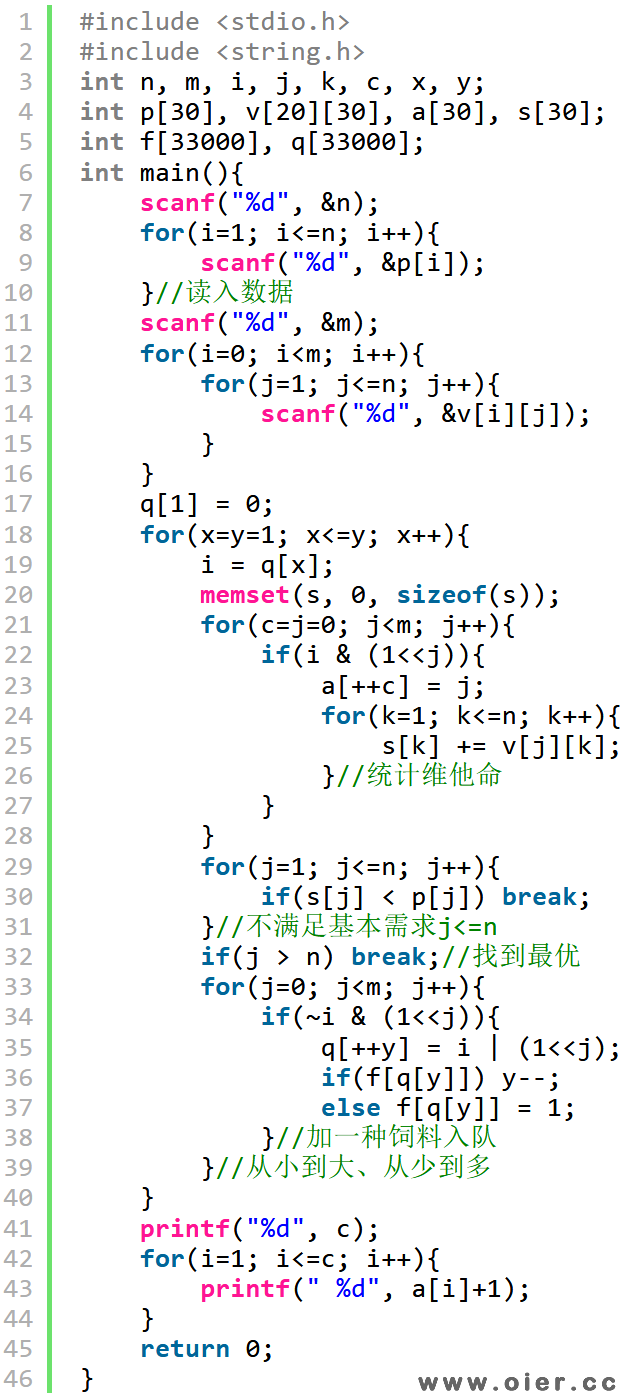
二进制暴力枚举,对应位置的1表示选择对应位置的饲料,接着还是统计维他命、记录最优值、最优方案。
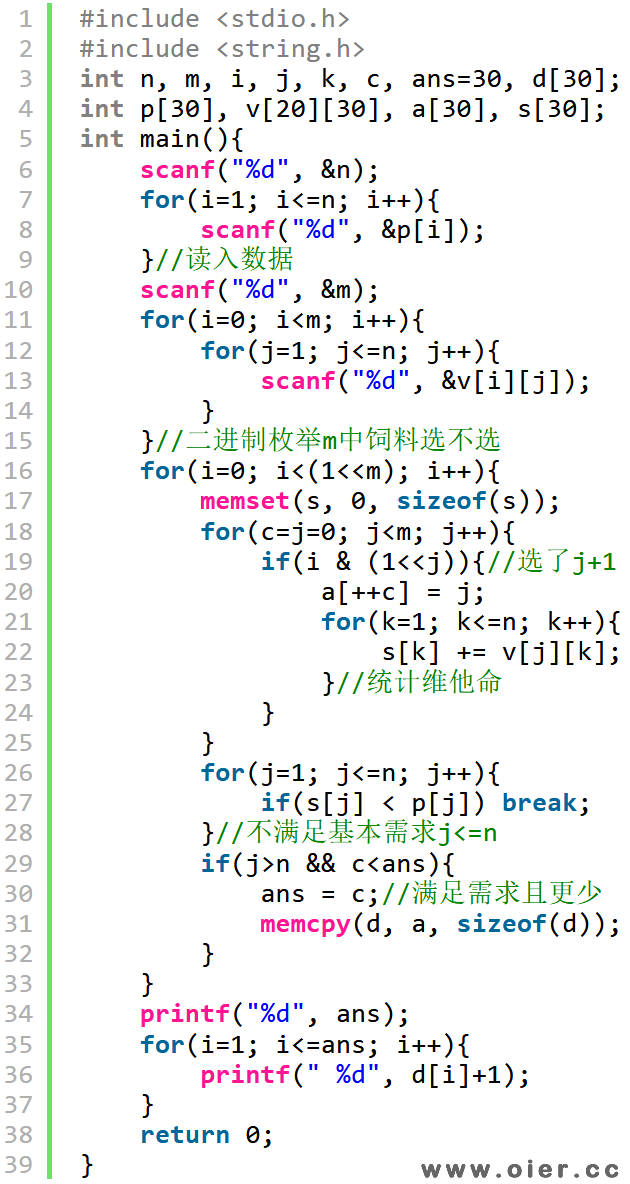
二进制+广搜,一开始一种饲料都不选,然后选1种饲料,再接着选2种饲料……直到选择c种饲料满足需求为止。需要保证从小到大枚举,字典序才满足要求,即|1的时候应从小到大;还有就是去重,两个1的可以有两种途径|出来,两个位置的单个1分别或另外一个1,三个1的方案就更多了,避免队列中出现重复状态,定义f数组记录数字是否入队过,入队过的话不再入队。