SSOJ1078牛式[USACO]
4498+
作者:crxis 发布:2018-09-14 分类:枚举
题目大意:对于一个有15个格子的乘法竖式,只允许用n种数字填写,有多少中填写方案?
题目描述
下面是一个乘法竖式,如果用我们给定的那n个数字来替代*,可以使式子成立的话,我们就叫这个式子牛式。
***
x **
----------
***
***
----------
****
数字只能取代*,当然第一位不能为0,况且给定的数字里不包括0。
注意一下在美国的学校中教的“部分乘积”,第一部分乘积是第二个数的个位和第一个数的积,第二部分乘积是第二个数的十位和第一个数的乘积.
写一个程序找出所有的牛式。
输入
Line 1:数字的个数n。
Line 2:N个用空格分开的数字(每个数字都属于{1,2,3,4,5,6,7,8,9})。
输出
共一行,一个数字。表示牛式的总数。
样例输入
5
2 3 4 6 8
样例输出
1
解题思路
暴力枚举乘数的5个数字,复杂度是n^5,可以解决,只是代码很难写得优美。
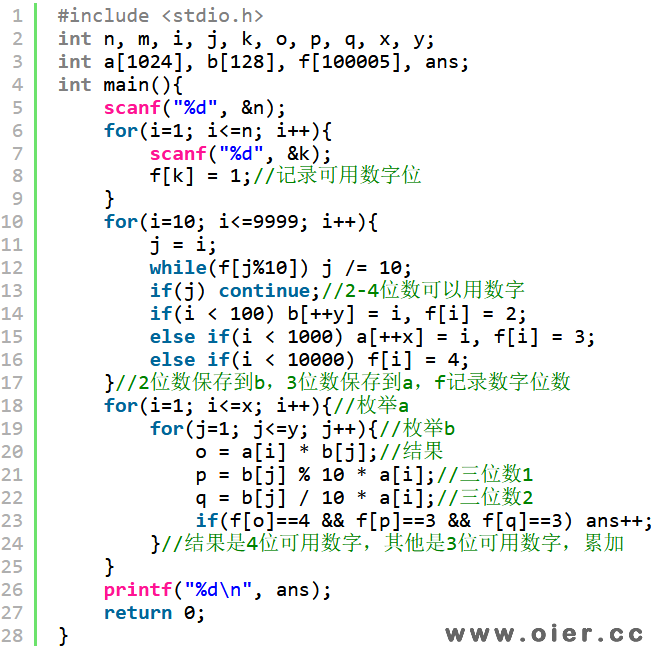
下面代码同样是枚举乘数a和乘数b,只是先把可以用数字按照位数存起来,f[i]非0表示数字i可以用,并存储i的位数。
将所有可用2位数保存到b数组,所有可用3位数保存到a数组,任何两两相乘,计算竖式对应的3个结果,如果都是可用数字且位数对得上,那就方案数加1。
程序实现