个人编程笔记

题目大意：n个数字，求区间中出现的数字种类的数量，即多次询问区间不同数字个数。

Given a sequence of n numbers a₁, a₂, …, a_n and a number of d-queries. A d-query is a pair (i, j) (1 ≤ i ≤ j ≤ n). For each d-query (i, j), you have to return the number of distinct elements in the subsequence a_i, a_i+1, …, a_j.

Input

• Line 1: n (1 ≤ n ≤ 30000).
• Line 2: n numbers a₁, a₂, …, a_n (1 ≤ a_i ≤ 10⁶).
• Line 3: q (1 ≤ q ≤ 200000), the number of d-queries.
• In the next q lines, each line contains 2 numbers i, j representing a d-query (1 ≤ i ≤ j ≤ n).

Output

• For each d-query (i, j), print the number of distinct elements in the subsequence a_i, a_i+1, …, a_j in a single line.

Example

Input
5
1 1 2 1 3
3
1 5
2 4
3 5

Output
3
2
3 

解题思路

1、暴力时间复杂度O(nm)，对于每个询问，暴力求区间不同数字数量，可以用桶排序，统计到1个的时候，增加1种数字。

2、暴力优化还是O(nm)，对于相邻两个询问，我们如果有重叠部分，可以不重复统计，如上一个询问是[5, 8]，下一个询问是[4, 9]，只需要l左移一位、r右移一位即可，但不能保证每次都可以这么“幸运”！

3、排序优化也是O(nm)，我们很容易想到按照左端点排序，这样左端点就好一直往右走，不回退；但是右端点，有可能一时是前10个，一时是后10个，这样每次来回扫描还是O(n)的。

4、分块排序$O((m+n)\sqrt{n})$，将左端点分成$\sqrt{n}$块，只要块号相同，就按照右端点排序。这样，对于每一块的询问，都是O(n)的。对于右端点，每块只会从左往右扫一遍，时间复杂度$O(n\sqrt{n})$；对于左端点，每次询问扫描的范围也只是$\sqrt{n}$，m次询问时间复杂度$O(m\sqrt{n})$。

赋初值：一开始随便统计一个区间即可，如区间[1, 1]，a[1]次数增加1，当前答案也是1。

程序实现

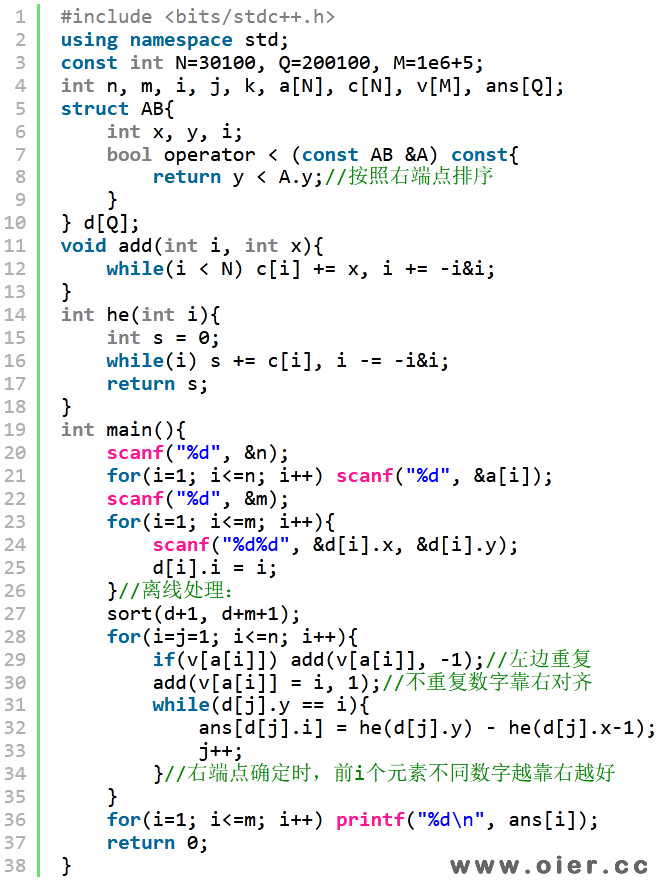
离线树状数组做法：按照右端点排序，重复数字只记录最右边的。

如区间[l, r]，右端点是r，那么左端点l不超过r，r前面的重复数字，显然越靠右边，越容易被统计。

如果没遇到重复数字，我们可以在该位置加1；如果遇到重复数字，把之前出现的位置减1（不统计左边的），再在新的位置加1，这样就能保证不重复统计。

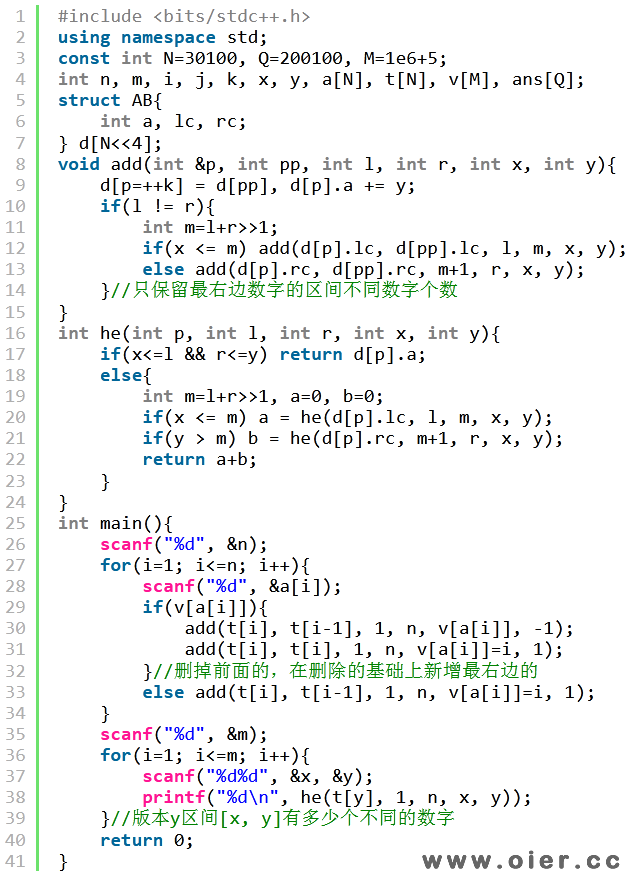
主席树做法：也是重复数字只记录最右边的。

修改函数：位置x增加y，那么新结点在原来基础上增加y，递归左子树或者右子树。

求和函数：区间[l, r]的不同数字数量，即插入第r个数字时，重复数字只保留最右边的线段树上区间[l, r]的和。