题目大意:电路中的电子元件需要一定的电流才能正常工作,已知知道电源+和-位置,以及各个元件两端电流流向及其最小电流,请问元器件都能正常工作吗?至少需要多少电流?[HDU3157]
Description
You’ve just built a circuit board for your new robot, and now you need to power it. Your robot circuit consists of a number of electrical components that each require a certain amount of current to operate. Every component has a + and a − lead, which are connected on the circuit board at junctions. Current flows through the component from + to − (but note that a component does not “use up” the current: everything that comes in through the + end goes out the − end).
The junctions on the board are labeled 1, …, N, except for two special junctions labeled + and − where the power supply terminals are connected. The + terminal only connects + leads, and the − terminal only connects − leads. All current that enters a junction from the − leads of connected components exits through connected + leads, but you are able to control how much current flows to each connected + lead at every junction (though methods for doing so are beyond the scope of this problem). Moreover, you know you have assembled the circuit in such a way that there are no feedback loops (components chained in a manner that allows current to flow in a loop).
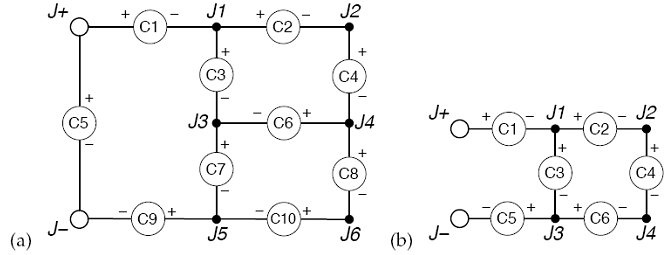
Figure 1: Examples of two valid circuit diagrams. In (a), all components can be powered along directed paths from the positive terminal to the negative terminal. In (b), components 4 and 6 cannot be powered, since there is no directed path from junction 4 to the negative terminal.
In the interest of saving power, and also to ensure that your circuit does not overheat, you would like to use as little current as possible to get your robot to work. What is the smallest amount of current that you need to put through the + terminal (which you can imagine all necessarily leaving through the − terminal) so that every component on your robot receives its required supply of current to function?
Input
Output
Sample Input
6 10 + 1 1 1 2 1 1 3 2 2 4 5 + - 1 4 3 2 3 5 5 4 6 2 5 - 1 6 5 3 4 6 + 1 8 1 2 4 1 3 5 2 4 6 3 - 1 3 4 3 0 0
Sample Output
9 impossible
Hint
解题思路
求有源汇有上下界的网络最小流,我们先把问题简单化,考虑是否存在可行流。
首先建图,+为源点S,-为汇点T,超级源点是SS,超级汇点是TT,读入m条边,a→b流量下界为c,上界无穷大,那么a到b建一条无穷大的边,并统计各点流入流出量;接着一个一个点(i)看,如果流入量为正,SS→i建边,如果流入量为负,i→TT建边,容量即流量绝对值;最后建立T到S的无穷大的边,转成无源汇网络流。
如何判断是否存在可行流?从SS到TT跑一遍网络最大流,如果流量刚好等于各点流入量之和,那么能满足下界要求,即存在可行流。此时,S流出量为所需电流量,都是由T流过来的,但它可能不是最小的。
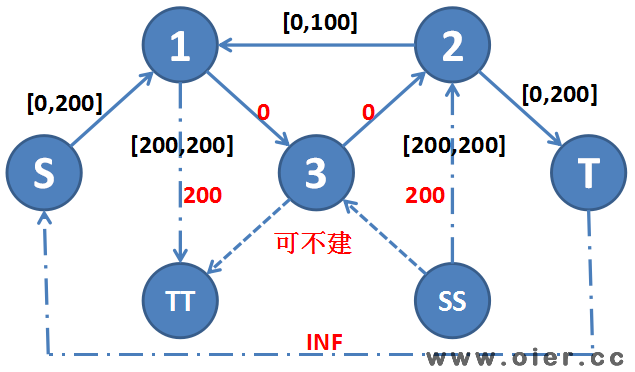
如图,SS→3以及3→TT的边可以不建,因为流入流出抵消了。此时从SS到TT跑网络最大流,可能这样流:SS→2→T→S→1→TT,流量为200。其实只需要100就够了,这样走流量才是最小的:SS→2→T→S→1→TT流量为100,SS→2→1→TT流量为100,满足下界要求,但从S只需要流出100而已。
也就是说,找到可行流之后,这个可行流可能不是最大的,要最大的话,需要从S到T继续跑网络流;同时,这个可行流也可能不是最小的,要最小的,就需要让自由流尽量的少。我们可以利用反向边,去掉超级源点和超级汇点以及T到S的边后,从T往S跑网络流,即让S流出量在满足下界的情况下更小。
跑完网络流后如何计算最小流?把S的出边的反向边的流量全部加起来即可,因为从S流出了多少,那么就有多少反向边流入到S。(当然,不算T→S的边)
程序实现
读入可以这样做:逐个字符读入,如果是正负号直接返回源点汇点编号,否则读到非空字符,就一直转到十进制整数s。
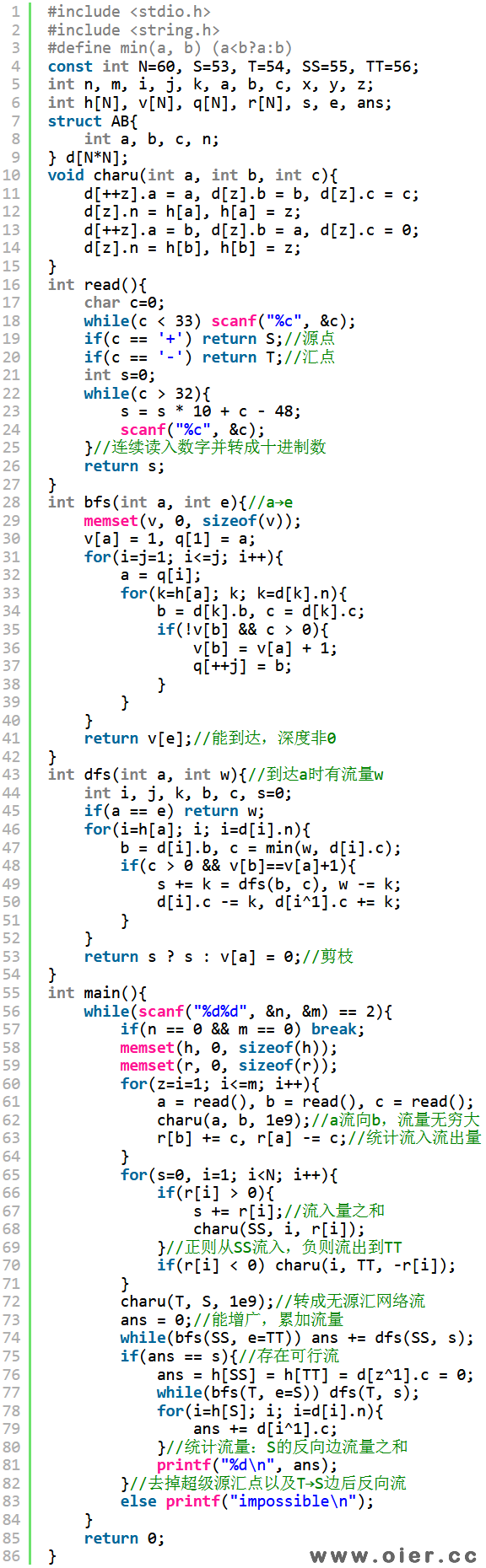
统计流量还可以这样做:第一次跑最大流,S的流出了就是T流向S的流量,即S→T这条边(d[z].c)的流量;第二次跑最大流,就是对之前流量的倒流,d[z].c减去第二次的流量即是最小流。

读入还能用sscanf,从字符串里面读入整数;当然,还有其他统计流量的方法:先不建T→S的边,跑一遍SS到TT的最大流,让其他边先用;再建立T→S的边继续跑,这样就不会出现T→S的流量先用的情况,后面就不需要减了。
