题目大意：一个n*n的点阵，站在左下角的点能直接看到其他点的个数是多少？

Description

A lattice point (x, y) in the first quadrant (x and y are integers greater than or equal to 0), other than the origin, is visible from the origin if the line from (0, 0) to (x, y) does not pass through any other lattice point. For example, the point (4, 2) is not visible since the line from the origin passes through (2, 1). The figure below shows the points (x, y) with 0 ≤ x, y ≤ 5 with lines from the origin to the visible points.

Write a program which, given a value for the size, N, computes the number of visible points (x, y) with 0 ≤ x, y ≤ N.

Input

Output

Sample Input

4
2
4
5
231

Sample Output

1 2 5
2 4 13
3 5 21
4 231 32549

解题思路

在同一条直线上的点，只有最近的一个点能直接看到，后面的点会被挡住。同一条直线上的点，与原点连线的斜率是一样的，也就是高度与宽度的比值是一样的。

不难发现，所有其他点与原点的练习，斜率都是y/x，如果y/x能约分，说明前面肯定有一个点挡住这个点。我们只需要求1到n中互质数对的个数即可求出答案，求一次的代价是O(n*n)，总的时间复杂度是O(c*n*n)会超时。

我们可以考虑用预处理的方法，依次推出1*1、2*2、3*3……每种询问的答案，时间复杂度就可以降低到O(n*n)了。

程序实现

水平和垂直方向各可以看到1个点，对角线上也可以看到1个点，对角线连边的斜线（点数）是对称的。我们可以先只算一个三角形（一半），最后输出结果的时候*2+1即可（1是对角线上的那个点）。显然，2*2包含了1*1看到的点，3*3包含了2*2看到的点，在计算面积大的之前，先赋值为前面面积小一点点的斜率数量，再枚举1到i-1的数字寻找互质数对，累加斜率数量即可。

上面的代码，第11-13行，其实是求与i互质的数字个数，即欧拉函数！欧拉函数可以通过质因数分解来快速计算出来。

首先，欧拉函数是积性函数，当a和b互质的时候，f(a*b) = f(a) * f(b)。求k的欧拉函数，将k进行质因数分解，若k=a^x*b^y*c^z，那么f(k) = f(a^x) * f(b^y) * f(c^z)。因为a是质数，当x==1时，f(a^1) = a-1；当x>1时，f(a^x) = a^x – a^x / a = a^x – a^(x-1) = a^(x-1)*x – a^(x-1)*1 = a^(x-1) * (a-1)。也就是说，质因子a的第一次幂*(a-1)，之和的次幂*a。

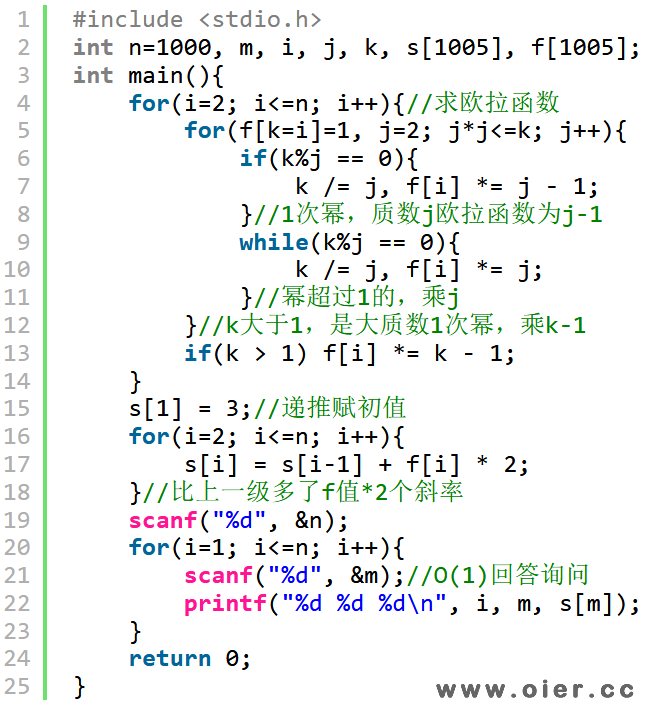
上面的代码，求欧拉函数，时间复杂度是O(n√n)，用线性筛还可以将复杂度降到O(n)。枚举2到n的数字，这些数字，乘以一个质数就可以得到一个合数，乘的质数，只要不大于其最小质因数，就能保证每个数字只被筛一次！因为每一个合数，分解成最小质因数和另外一个数的乘积，只有一种方案，也就是每个数最多只会被筛一次！

关键：遇到一个质数，存入s数组；枚举质数s[j]时，如果发现i%s[j]==0，也就是i中包含s[j]这个质因子，后面的质因子就不用乘了，此时合数i*s[j]应该累乘s[j]，因为合数中质因子s[j]的次幂大于1；否则累乘f[s[j，即s[j]-1。