题目大意：铺砖问题，即一个n*m的矩形，用1*2的砖铺满，共有多少种方案？[HDU1400]

Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his ‘toilet series’ (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

 

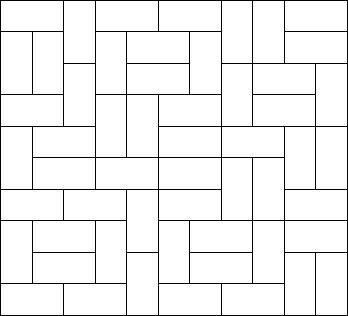
Expert as he was in this material, he saw at a glance that he’ll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won’t turn into a nightmare!

Input

Output

Sample Input

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

Sample Output

1
0
1
2
3
5
144
51205

解题思路

状态压缩，铺砖要么横着铺，要么竖着铺，横铺用0来表示，竖铺用1来表示。n行m列，那么状态范围是0到p=1<<m，f[i][j]表示前i-1行已经铺满，第i行的状态是j的方案数。

状态转移：当前行状态是j，前一行状态是k（k中0的位置，要么横铺，要么上上行竖着铺）。首先，竖着铺用1来表示，如果上一行竖着铺，那么下一行就不需要铺也不能够铺，即上下不能有相邻的1，j&k必须为0；其次，上一行竖着铺，那么下一行对应位置不需要铺横砖，这一行竖着铺，对应位置也不需要铺横砖，j|k后矩形范围内0的位置都需要铺横砖，即0的位置必须两个两个分别连在一起才有可能铺成，如何判断能否铺成呢？将0转成1，1转成0后，就可以转成判断两个两个1分别连在一起，判断方法可以是每次取出2个1，如果两个1不成2倍关系即不可行，如果只能取出1个1也不可行，其余情况可行，全部铺横砖共有1种方案。

加法原理：当前状态有上一行状态转移过来，当前行状态确定，铺法唯一，上一行每一个状态都是相互独立不重复的，方案数量累加起来；乘法原理：一行的状态，有横铺和竖铺组成，方案数为横铺*竖铺的方案数，因为横铺方案唯一，故只需要竖铺的方案（状态确定，竖铺方案也唯一）。

程序实现

预处理每个状态是否可横铺，省去log的时间，快20%：