POJ2104K-thNumber
5936+
作者:crxis 发布:2021-01-11 分类:线段树
题目大意:n个数,m个询问,每次询问区间[l, r]直接第k小是多少?
Description
You are working for Macrohard company in data structures department. After failing your previous task about key insertion you were asked to write a new data structure that would be able to return quickly k-th order statistics in the array segment.
That is, given an array a[1…n] of different integer numbers, your program must answer a series of questions Q(i, j, k) in the form: “What would be the k-th number in a[i…j] segment, if this segment was sorted?”
For example, consider the array a = (1, 5, 2, 6, 3, 7, 4). Let the question be Q(2, 5, 3). The segment a[2…5] is (5, 2, 6, 3). If we sort this segment, we get (2, 3, 5, 6), the third number is 5, and therefore the answer to the question is 5.
That is, given an array a[1…n] of different integer numbers, your program must answer a series of questions Q(i, j, k) in the form: “What would be the k-th number in a[i…j] segment, if this segment was sorted?”
For example, consider the array a = (1, 5, 2, 6, 3, 7, 4). Let the question be Q(2, 5, 3). The segment a[2…5] is (5, 2, 6, 3). If we sort this segment, we get (2, 3, 5, 6), the third number is 5, and therefore the answer to the question is 5.
Input
The first line of the input file contains n — the size of the array, and m — the number of questions to answer (1 <= n <= 100 000, 1 <= m <= 5 000).
The second line contains n different integer numbers not exceeding 109 by their absolute values — the array for which the answers should be given.
The following m lines contain question descriptions, each description consists of three numbers: i, j, and k (1 <= i <= j <= n, 1 <= k <= j – i + 1) and represents the question Q(i, j, k).
The second line contains n different integer numbers not exceeding 109 by their absolute values — the array for which the answers should be given.
The following m lines contain question descriptions, each description consists of three numbers: i, j, and k (1 <= i <= j <= n, 1 <= k <= j – i + 1) and represents the question Q(i, j, k).
Output
For each question output the answer to it — the k-th number in sorted a[i…j] segment.
Sample Input
7 3 1 5 2 6 3 7 4 2 5 3 4 4 1 1 7 3
Sample Output
5 6 3
Hint
This problem has huge input,so please use c-style input(scanf,printf),or you may got time limit exceed.
Source
Northeastern Europe 2004, Northern Subregion
解题思路
区间第k小,可以用线段树解决:
结点记录区间[l, r]数字的数量,左儿子记录区间[l, m]数字的数量x,右儿子记录区间[m+1, r]数字的数量y。如果k不超过x,那么在左儿子找第k个,否则在右儿子找第k-x个。
现在的问题是,区间很多个!我们可以用可持久化线段树(主席树)来记录历史版本。对于求数据区间[a, b]的第k小,首先我们需要知道区间[a, b]有多少个数,左儿子有多少个数,这里可以用前缀和的思想:s[b] – s[a-1]即可知道这个区间的数字数量,其中a、b是时间,记录该时间点的数字数量。
最后是考虑如何建立线段树:每次插入一个数,都需要新建一条链的结点,因为该条链发生了修改。对于没发生修改的,保持不变即可。
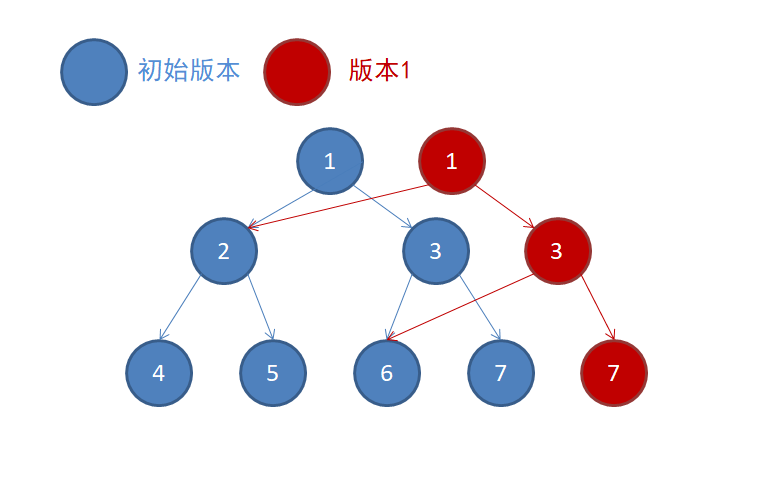
如结点7数量增加1,那么发生改变的是节点1、3、7,我们动态开点存储即可,根结点需要再开一个头指针存储。
程序实现
